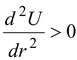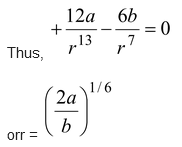Conservative Forces and Potential Energy Functions

We now consider how we can find a conservative force if we are given the associated potential energy function. According to equation (8.2), an infinitesimal change in potential energy dU is related to the work done by the conservative force Fcin an infinitesimal displacement ds as follows

dU = −(8.17)

In one dimension, the above equation reduces to dU = −Fxdx

Thus,Fx= -dU/dx (8.18)

Let us see how equation (8.18) can be used for the common known cases:

For gravitational potential energy,

Ug= mgyFy= − dU/dx = -mg

For spring potential energy,

US= 1/2kx₂ Fx= -dU/dx = -kx

A conservative force can be derived from a scalar potential energy function

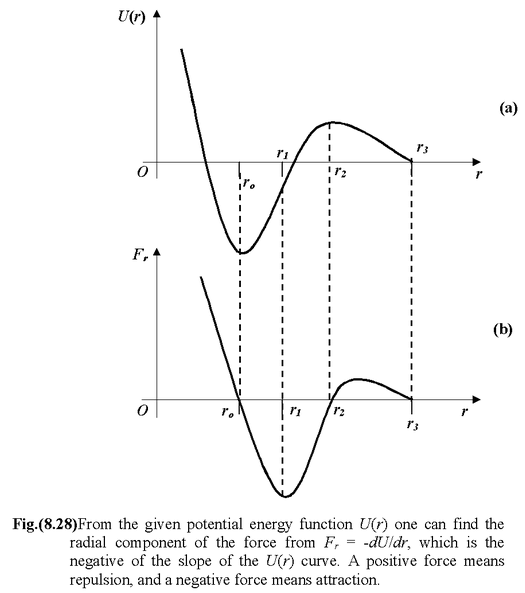
Consider an arbitrary potential energy function U(r) as shown in figure (8.28 a).

The radial component of the associated conservative force is negative of the slope of the potential energy function, that is

Fr= -dU/dx

The force function may be plotted qualitatively as shown in the figure (8.28 b). If Fr> 0, the force is directed toward positive r, which means repulsion, whereas Fr< 0 means attraction.

The following important points can be easily noticed by looking at the potential energy and force diagrams.

(r > r₂): Fr> 0The particle is weakly repelled.

(r = r₂): Fr= 0. At the maximum point of the potential energy function, the particle would be in unstable equilibrium. If the particle were slightly displaced either to the left or to the right, it would tend to move away from this point.

(ro < r < r₂): Fr< 0. The force is attractive, being strongest at r1where the slope is greatest.

(r = ro): Fr= 0. At the minimum point of the potential energy function, the particle would be in stable equilibrium. If slightly displaced in either direction, it would tend to return to this point.

(r < ro): Fr> 0. The particles repel each other. The repulsive force becomes stronger as r is reduced (since the slope of U(r) gets steeper).

Example 8.15

The potential energy function for the force between two atoms in a diatomic molecule can be expressed approximately as

U(r) =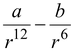

where a and b are constants and r is the separation between the atoms.

(a)Determine the force function F(r).

(b) Find the value of r for which the molecule will be in the stable equilibrium.

Solution

(a)The force between the two atoms is given by

F(r) = -dU/dr

orF(r) =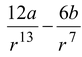

(b)For stable equilibrium F(r) = 0 and