Chord of contacts

Chord of Contact

If the circle is x² + y² + 2gx + 2fy + c = 0

and if tangents have been drawn from an external point A(x₁, y₁) touching the circle at B and C then the equation of BC (chord of contact) is T = 0 and is written as,

xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0

Length of the tangent in the general case from a point (x1, y1)

=

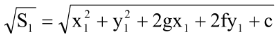
Orthogonality of two circles is given by

S₁ = x² + y² + 2g₁x + 2f1y + c₁

and S₂ = x² + y² + 2g₂x + 2f₂y + c₂

the condition 2g₁g₂ + 2f₁f₂ = c₁ + c₂