Different forms of the equation of circles
Circles of Class 11
Different Forms of the Equation of a circle
(a) (x - α)2 + (y - α)2 = α2 is a circle with centre (α, α) and radius = α touching both the axes.
(b) (x - α)2 + (y - β)2 = β2 touches the x – axis.
(c) (x - α)2 + (y - β)2 = α2 touches the y - axis.
(d) x2 + y2 - αx - βy = 0 is with centre (α/2,β/2) and
radius = 
. It passes through (0, 0), (α, 0) and (0, β).
Equation of the tangent to the circle
x2 + y2 + 2gx + 2fy + c = 0 at the point (x1, y1) is xx1 + yy1 + g(x + x1) + f(y + y1) + c = 0
and that of the normal is y – y1 =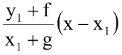 
In particular to the circle x2 + y2 = r2 at (x1, y1), the equation of tangent is
xx1 + yy1 = r2 and the normal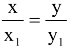 
.
Normal to the circle always passes through the centre.
