General equation of a line with slope
Circles of Class 11
General equation of a line with slope m and which is a tangent to the circle
x2 + y2 + 2gx + 2fy + c = 0 is
(y + f) = m(x + g) ± 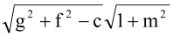
Which reduces to y = mx ± a 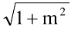
in case of circle x2 + y2 = a2
The locus of the point of intersection of the two perpendicular tangents is called the ‘Director Circle’ and is x2 + y2 = 2a2 for the circle x2 + y2 = a2. In general director circle in case of circles is a concentric circle with radius √2 times the original circle.
Equation of the chord of the circle
x2 + y2 + 2gx + 2fy + c = 0
in terms of its midpoint (x1, y1) is T = S1
Where T = xx1 + yy1 + g(x + x1) + f(y + y1) + c
and S1 = x12 + y12 + 2gx1 + 2fy1 + c









