Common Tangents

Common Tangents

Find T, using 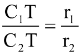(internally) and D, using 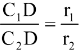(externally)

To find equations of common tangents

Assume the equation of the tangent of any circles (from given two points) in the form (y + f) = m(x+ g) + r1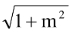. (Here (−g,−f) is center of first circle with radius r1)

T and D will satisfy the assumed equation.

Thus obtain m, and now we can find the equation of the tangents passing through T and D.

(x – x₁)² + (y – y₁)² + λ{(y – y₁) – m(x – x1)}= 0

is the family of circles which touch y – y1 = m(x – x₁) at (x₁, y₁) for any finite m

If m is infinite the family reduces to (x – x₁)² + (y – y₁)² + λ(x – x₁) = 0.

Radical Axis

The equation of radical axis of two circles S1 = 0 and S2 = 0 is given by S1- S2 = 0

(Coefficient of x₂ and y₂ being 1 for both the circles).

Radical Centre

The common point of intersection of the radical axes of three circles taken two at a time is called the radical centre of the three circles.