Classification of Function

Function can be classified into two categories:

1. One-one or Many-one
2. Into or Onto

Each of above category comprises entire gamut of function. Thus if a function is not one-one, it has to be many-one and vice-versa.

Similarly if function is into then it cannot be onto and converse.

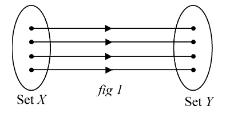
(i) One-one functions (Injective)

A function is said to be one - one if for every value of x in the Domain, there exists one and only one value in co-domain.

Note

Two different values of x do not have same value of y.

e.g.

(a) f(x) = 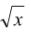is one to one on any domain of non-negative numbers because  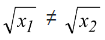whenever x1 ≠ x².

(b) g(x) = sin x is not one-to-one because for many different values of x we get same value of g(x).

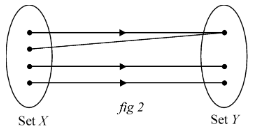
(ii) Many-one functions

A function is said to be many-one if there exists at least two elements in domain which have same image in co-domain.

(iii) Into functions

(b) g(x) = sin x is not one-to-one because for many different values of x we get same value of g(x).

(ii) Many-one functions

A function is said to be many-one if there exists at least two elements in domain which have same image in co-domain.

(iii) Into functions

If there exist at least one element in co-domain which doesn't have a pre-image then such function are said to be into.

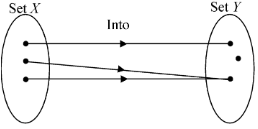
(iv) Onto functions (Surjective)

If there doesn't exist any element in co-domain which does'nt have a pre-image then such functions are said to be onto. Note that for onto function co-Domain ≡ Range.

Based on above two categories of function, we can classify the function into four type

(i) One-one and Onto (Bijective)

(ii) One-one and Into

(iii) Many-one and Onto

(iv) Many-one and Into.