Methods to find domain and rang of a function

Methods to find domain and rang of a function

By definition, domain of a function are those values of 'x' (Independent variable) for which f(x) exists or is defined.

If a function is expressed as sum, difference, product or division of two or more functions then the domain of function can be defined by the following method:

Let f : D₁  → R and g : D₂ → R.

Let D₁ ∩ D₂ = D. Then we describe functions f + g, f - g, gf and f/g as follows

(1) f + g : D → R is a function defined by (f+g)(x) = f(x) + g(x)

(2) f - g : D → R is a function defined by (f - g) (x) = f(x) - g(x)

(3) fg : D → R is a function defined by (f g) (x) = f(x) g(x)

(4) f/g : C → R is a function defined by (f/g) (x) =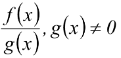

where C = {x ∈ D : g(x) ≠ 0}.