Inverse of a function

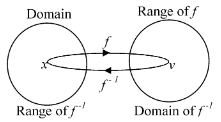
Inverse of a function

y ∈ Y, g(y) = x ⇔ y = f(x). The function g so defined is called the inverse of f. And now f and g are inverse to each other. If f and g are inverse to each other then f(g(x)) = g(f(x)) = x.

How To Find f -1

Let f : X → Y be a function defined by y = f(x) such that f is both one-one and onto
(i.e bijective). Then there exists a unique function g : Y → X such that for each

Step 1: Solve the equation y = f(x) for x in terms of y.

Step 2: Interchange x and y. The resulting formula will be y = f -1(x).

e.g. Inverse of y = 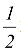x + 1

Step 1: x = 2y - 2

Step 2: y = f-1(x) = 2x - 2

Which is inverse of f(x) = 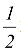x + 1

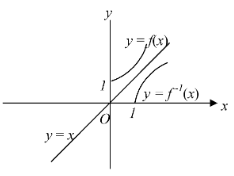
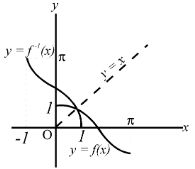
How To Draw Graph Of f -1

Since g(y) = x,

⇒ g[f(x)] = x ⇒ g′[f(x)] × f ′(x) = 1

or g′(y) = .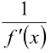

Hence 'g' and 'f ' are mirror images of each other w.r.t line y = x. Geometrically the graph is symmetric about the line y = x.