Various type of function

Various type of function

(a) Even and Odd Functions

A function y = f (x) is even if f (−x) = f (x) for every number x in the domain of f.

e.g. f (x) = x² is even because f (−x) = (−x)² = x² = f (x).

A function y = f (x) is odd if f (−x) = −f (x) for every x in the domain of f.

e.g. f (x) = x³ is odd because f (−x) = −x³ = −f (x).

Note: (1) For Domain 'R', even functions are not one−one.

(2) Every function can be written as a sum of even and odd functions.

(3) f (x) = 0 is the only function which is both even and odd.

(4) Every odd continuous function passes through origin.

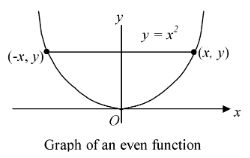
(5) The graph of an even function y = f (x) is symmetric about the y-axis. Equivalently
(x, y) lies on the graph ⇔ (−x, y) lies on the graph.

(6) The graph of an odd function y = f (x) is symmetric about origin. i.e. if point (x, y) is on the graph of an odd function, then (−x, −y) will also lie on the graph.

Application 5 Determine whether the function, f(x) = is even, odd or neither of the two.

Solution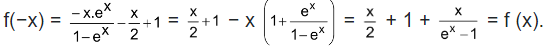

Hence the given function is even.

Rules for finding period of a periodic function

(i) If f(x) is periodic with period p, then af(x) + b, where a, b ∈ R (a ≠ 0) is also a periodic function with period p.

(ii) If f(x) is periodic with period p, then f(ax + b), where a ∈ R\{0} and b ∈ R, is also periodic with period p/|a|.

(iii) If f(x) is periodic with p as the period and g(x) is periodic with q as the period
(p ≠ q) and L.C.M. of p & q is possible, then f(x) + g(x) is periodic with period equal to L.C.M. of p & q, provided f(x) and g(x) cannot be interchanged by adding a positive number in x which is less than L.C.M. of p & q in this case this number becomes period of f(x) + g(x).

(iv) If f(x) is periodic with period p, then I/f(x) is also periodic with same period p.

(v) If f(x) is periodic with period p, 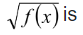 also periodic with same period p.

(vi) If f(x) is a periodic function with period p and g(x) is a strictly monotonic function, then g(f(x)) will also be periodic with period p.

(vii) Constant function is periodic with no-fundamental period.

(c) Equal or Identical functions

Two functions 'f ' and 'g' are said to be equal iff they satisfy the following conditions:

(i) They have same domain.

(ii) They have same range.

(iii) f = g for all values of 'x' in their common domain.

e.g f (y) = 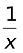and g (x) = 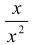are equal functions.

(d) Homogeneous function

A function with one or more than one independent variable and such that every term has the same degree is called as a homogeneous function.

e.g. f (x, y) = x² − xy + 3y² is a homogeneous function of degree '2'.