Application of Vectors to Geometry
Share
Application of Vectors to Geometry
Vector of Class 12
Application of Vectors to Geometry
(a) Bisectors of an angle between the line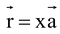 
and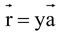 
are given
by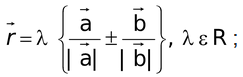 
+ sign give internal bisector and – sign gives external bisector.
(b) Section Formula
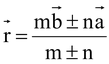, ± representing internal and external division.
(c) Equation of straight line
(i) Vector equation of the straight line passing through origin and parallel to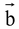 
is given by 
, t being scalar.
(ii) Passing through the point whose position vector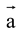 
and parallel to the vector
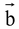is given by 
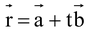, t being scalar.
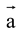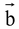(iii) Passing through the points whose position vector are and is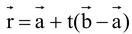 
, t being scalar.
(d) Equation of a Plane
Equation of a plane passing through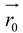 
and having a normal vector 
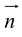is given as 
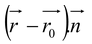= 0.
Note that the plane ax + by + cz + d = 0 has a normal vector as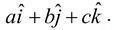 
.
(i) Perpendicular distance of the line
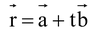from the point P (PV being 
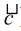) is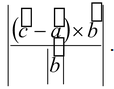 
.
(ii) Perpendicular distance of the plane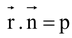 
from the point p (pv )
= 
.
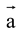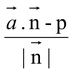The condition that two lines
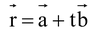and 
are coplanar is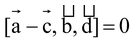 
The shortest distance between two non-intersecting lines (Skew lines). 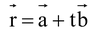and is given by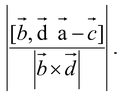 
.
