DISTANCE BETWEEN TWO POINTS

Distance Formula :

The distance between any two points in the plane is the length of the line segment joining them.

The distance between two points p(x₁, y₁) and Q(x₂, y₂) is given by

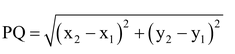
i.e.

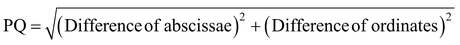
Now, we have to find the distance between two points P(x₁, y₁) and Q(x₂, y₂). PR and QS perpendiculars have been drawn to the x-axis. A perpendicular from the point P on QS is also drawn which meets at T in figure.

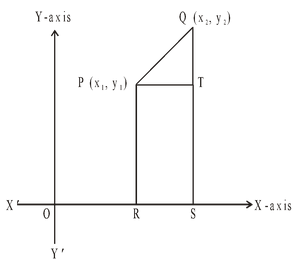
OR = x₁, OS = x₂

RS = x₂ – x₁

=> PT = x₂ – x₁[ RS = PT]

Again, PR = y₁, QS = y₂

QT = y₂ – y₁

Now, in right 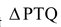, we have

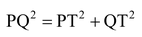
[By Pythagoras Theorem]

=> PQ2 =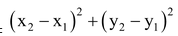

Hence, PQ =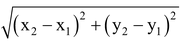

It is called distance formula.

N.B. The distance is always non-negative, so we take only the positive square root.

LEARN IT

(i) The distance of a point P(x, y) from the origin O(0,0) is given by

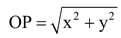
(ii) We can also write :

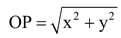
Because the value of x₁ – x₂ will always be negative and its square will be positive. Similarly, the value of y1 – y2 will always be negative and its square will be positive.

Hence, there will not be any change in the value of both the formulae.

question. Find the distance between

(i) (5,3) and (3,2) (ii) (-1,4) and (2,-3) (iii) (a,b) and (-b,a)

Solution: Let d₁, d₂, d₃ be the required distances. By using the formula, we have

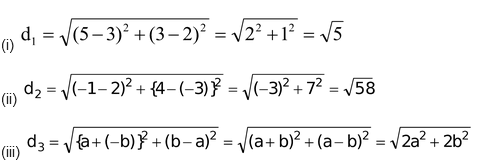
Things to remember 

1.With the help of distance formula we can find triangle is

1. Equilateral

2.Right Angle

3.Isoseles 

2.With the help of distance formula we can find quadrilateral is

1.Square 

2.Rectengle

3.Rombus

4.Parrellogram 

eg

question. Prove that the point (1, 2), (2, 4), (8, 1) and (7, -1) are the vertices of a rectangle.

Solution: Let P(1, 2), Q(2, 4), R(8, 1) and S(7, -1) be the given points

Hence, the opposite sides are equal.

Again, diagonal PR = SP

Hence the diagonals are equal.

Hence the given point P, Q, R, S are the vertices of rectangle.