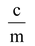GRAPH OF LINEAR EQUATION ax + by + c1 = 0

Graph

ax + by + c₁ = 0

Steps to draw linear equation graph.

Step 1. Arrange the terms to find the value of y in terms of x

i.e. y = mx + c form

where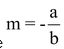 and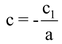

Step 2. Assume three integer values of x, and get the corresponding values of y.

Step 3. Prepare a table for the ordered pairs (x, y).

Step 4. Plot these points on a graph paper by considering suitable scale.

Step5. Join these points to obtain the graph of the line ax + by + c1 = 0.

question Draw the graph of the line y = mx + c.

Solution: y = mx +c

∴ Required table is

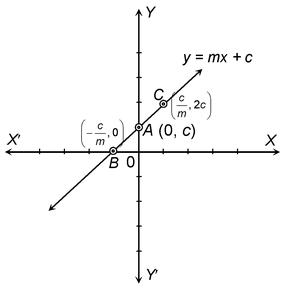
1. The graph of the line changes if the signs of m and c differ.

2. Here m (the coefficient of x) in the equation y = mx + c is known as slope of the line.

3. c is known as intercept on y-axis i.e., OA = c.

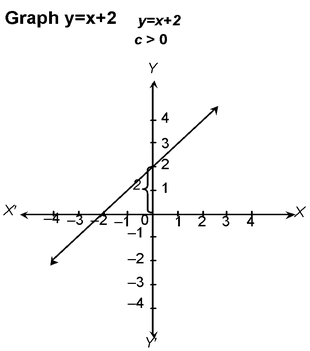
eg. Draw the graph of y= x +2 

Step 1. Arrange the terms to find the value of y in terms of x

i.e. y = x +2 form

where m = 1 and c = 2

Step 2. Assume three integer values of x, and get the corresponding values of y.

Step 3. Prepare a table for the ordered pairs (x, y).

Step 4. Plot these points on a graph paper by considering suitable scale.

Step 5. Join these points to obtain the graph of the line ax + by + c1 = 0.

∴ Required table is

SECTION FORMULA :

A point P divides the straight line joining two points A(x1, y1) and B(x2, y2) internally in the ratio m1 : m2, to find the coordinates of P.

Let the coordinate of P be (x, y). AR, BT and PS perpendiculars have been drawn on the X-axis from A, B and P respectively. Now, AQ and PC perpendiculars have been drawn from A and C on PS and BT respectively. In figure.

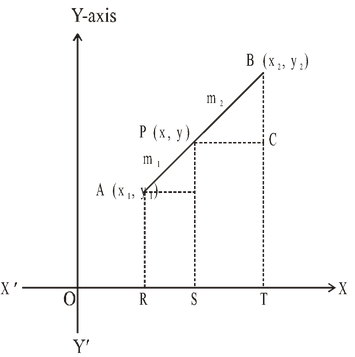
AQ = RS = OS – OR = x – x1,

PC = ST = OT – OS = x₂ – x,

PQ = SP – SQ = SP – RA = y – y1, and 

BC = TB – TC = TB – SP = y₂ – y.

Now, from similar triangles APQ and PCB, we have,

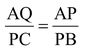
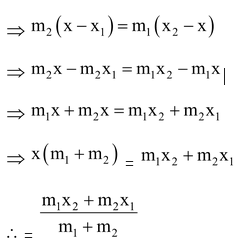
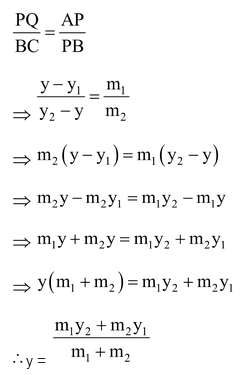
Hence, the coordinates of point P which divide the straight line joining two points (x₁, y₁) and (x₂, y₂) internally in the ratio m1 : m2 are,

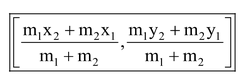
Coordinates of the Mid-Point :

If P is the mid-point of AB, then it will divide AB in the ratio of 1 : 1, then coordinates of P are :

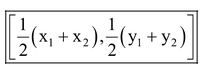
question. If the point C(–1, 2) divides internally the line segment joining A(2, 5) and B in ratio
3 : 4, find the coordinates of B.

Solution: Let the coordinates of B be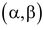 in figure. It is given that AC : BC = 3 : 4. So, the coordinates of C are :

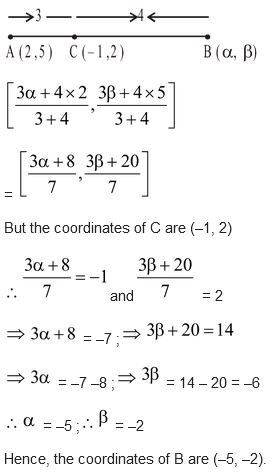
CENTROID:

The point of the intersection of the medians of a triangle is called centroid of a triangle. 

Theorem :

Prove that the coordinates of the centroid of the triangle whose vertices are (x₁, y₁), (x₂, y₂) and (x₃, y₃) are 

. 

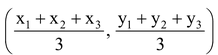Also, deduce that the medians of a triangle are concurrent. 

Proof: Let A(x₁ , y₁) B(x₂ , y₂) and C(x₃, y₃) be the vertices of ΔABC whose medians are AD, BE and CF respectively. So, D, E and F are respectively the mid points of BC, CA and AB. 

Coordinates of D are . 

Coordinates of a point dividing AD in the ratio 2 : 1 are 

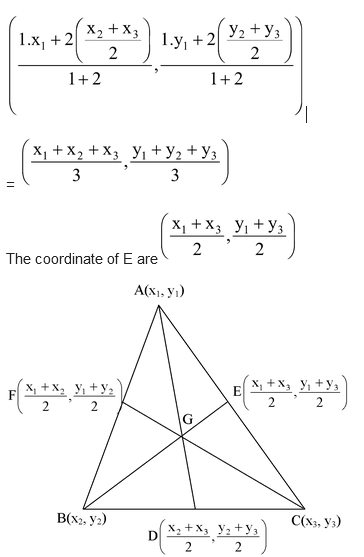
The coordinates of a point dividing BE in the ratio 2 : 1 are 

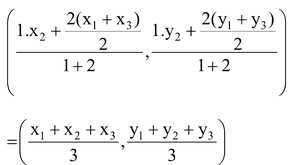
Similarly the coordinates of a point dividing CF in the ratio 2 : 1 are 

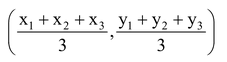
Thus, the point having coordinates coordinate geometry 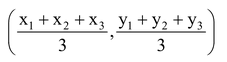is common to AD, BE and CF and divides them in the ratio 1 : 2. 

Hence, medians of a triangle are concurrent and the coorrinates of the centroid are .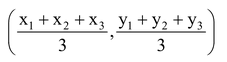

question. Find the coordinates of the centroid of a triangle whose vertices are (0, 6), (8, 12) and (8, 0). 

Solution: We know that the coordinates of the centroid of a triangle whose angular points are (x1, y1) (x2, y2), (x3 , y3) are 

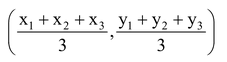
So, the coordinates of the centroid of a triangle whose vertices are (0, 6), (8, 12) and (8, 0) are 

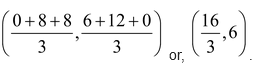
AREA OF A TRIANGLE:

We have already studied in previous classes about how to calculate the area of a triangle when its base and corresponding height altitude are given.

We have used the formula :

Area of triangle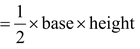

Besides this, we have also studied in previous class about how to find the area of a triangle by using “Heron’s Formula”, When the length of the sides are given.

i.e., Area of a triangle 

.

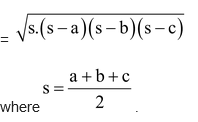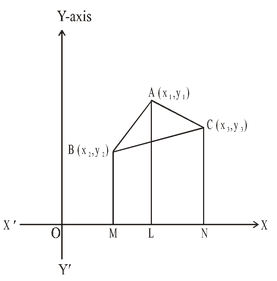
Let A(x1, y1), B(x2, y2) and C(x3, y3) be the vertices of . AL , BM and CN perpendiculars have been drawn from A, B, C to the X-axis.

Area of = Area of trapezium ABML + Area of trapezium ALNC – Area of trapezium BMNC

We know that :

The area of a trapezium 

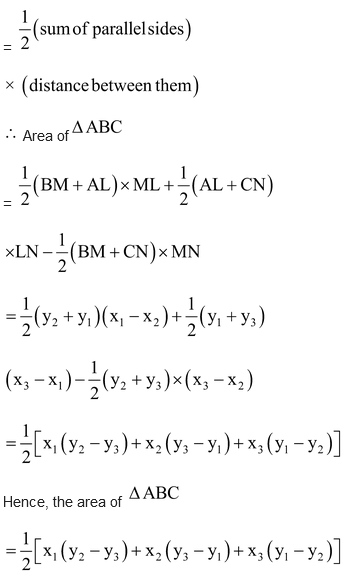
question. Find the area of the triangle formed by the points A(5, 2), B(4, 7) and C(7, –4).

Solution: Here, x1 = 5, y1 = 2, x2 = 4, y2 = 7, x3 = 7 and y3 = –4.

∴Area of

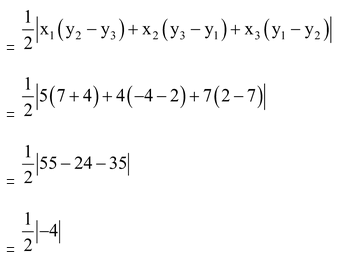
Hence, area of = 2 sq.units.

question. Prove that the point (-2, -1), (-1, 1), (5, -2) and (4, -4) are the vertices of a rectangle.

Solution: Let P(-2, -1), Q(-1, 1), R(5, -2) and S(4, -4) be the given points

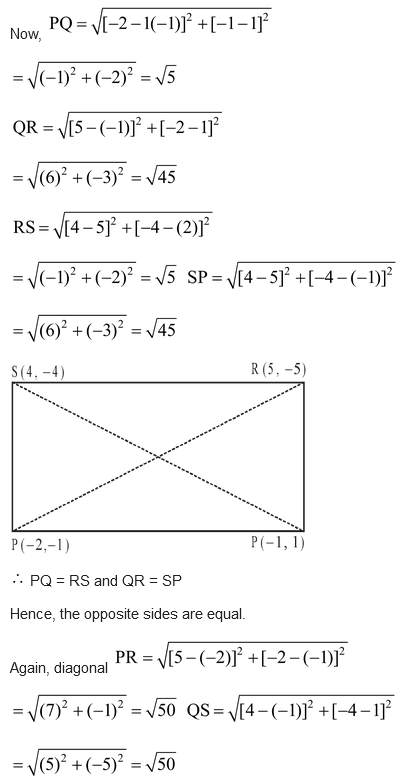
Hence the diagonals are equal.

Hence the given point P, Q, R, S are the vertices of rectangle.