Grouping Of Identical Cells

GROUPING OF IDENTICAL CELLS

Illustration 26.A cell has an emf of 5.0 volt and an internal resistance of 1.0 Ω.  Its terminals are joined through a 9 Ω resistor.  Calculate the potential difference across the terminals.

Solution:I =

V = E – Ir = 5 − 1/2 x 1

V = 4.5 volt.

Illustration 27.Six lead−acid type of secondary cells, each of emf 2.0 V and internal resistance 0.015 Ω, are joined in series to provide a supply to a resistance of 8.5 Ω.  Determine 

(i) current drawn from the supply and (ii) its terminal voltage.

Solution:emf of series combination of cells = (6 × 2 )V = 12 V.

Total internal resistance of series combination = 6 × 0.015 Ω = 0.09 Ω

External resistance = 8.5 Ω

Total resistance of circuit = (8.5 + 0.09)Ω = 8.59 ohm.

Total current (I) = Total emf/Total resistance = 12/8.59 A = 1.4 A

Terminal potential difference = (12 – 14 × 0.09) volt =11.9 volt.

Illustration 28.In a series grouping of N cells, current in the external circuit is I. The polarity of how many cells should be reversed so that the current becomes (1/3)rd  of the earlier value?

Solution:Before reversing the polarity of the cells, the current is

I = NE/R + Nr

Let n cells be reversed in their polarity

∴ Net e.m.f.  = (N – n)E – nE= (N−2n) E

Total resistance = Nr + R

⇒ n =N/3, 

This is valid only when N is a multiple of 3, otherwise it cannot be done.

Parallel Grouping

Let us assume that there are n rows and each single row contains battery of emf E and internal resistance r, as shown in the figure.

Applying Kirchhoff’s law, to the equivalent circuit

       ⇒

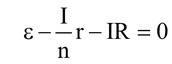• To get maximum current, cells must be connected in series if effective internal resistance is less then external resistance, and in parallel if effective internal resistance is greater than external resistance. 

Mixed grouping

Let us assume, that each branch of the circuit contains n batteries of emf E and internal resistance r and there are m such rows as shown in the figure.

Number of rows is m and number of cells in each row is n.

Applying Kirchhoff’s law to the equivalent circuit.

Effective grouping of cells

For effective grouping, current should be maximum 

⇒ mR + nr  should be minimum 

Now,mR + nr =

The second term is non−zero, the term in the parenthesis = 0

⇒  mR = nr⇒R = (n/m)r

Illustration 29. There are 27 cells with an internal resistance 0.4 Ω and an external resistance 1.2 Ω. What is the most effective way of grouping them?

Solution:Let there be n cells in series having m parallel branches

mn = 27…  (1)

mR = nr… (2)

1.2 m = n (0.4)

⇒  3m = n… (3)

From equations (1) and (3) , we get m= 3 and n = 9