A Conductor In An Electrostatic Field
Electrostatics of Class 12
On the basis of their conductivity all bodies can be divided into two classes: conductors and dielectrics (also called insulators). In conductors electric charges are free to move throughout the volume of such bodies. In dielectrics, on the contrary, the charges remain fixed at the places where they were initially distributed.
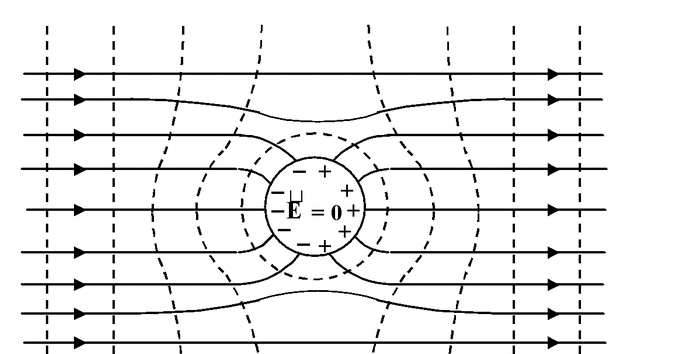
Inside a conductor the field strength equals zero (E= 0). If this were not so, an ordered motion of the charges would occur in the conductor without any expense of energy from an external source. But this contradicts the law of conservation of energy. Hence the field strength within a conductor E inside = 0
It follows that all points of a conductor have the same potential and the surface of a conductor is an equipotential surface. This fact implies that the field lines are perpendicular to a conducting surface. If the opposite were true, the tangential component of E would make the charges move over the surface of the conductor, i.e. charge equilibrium would be impossible.
Furthermore, since E = 0 everywhere in the conductor, the density of excess (uncompensated) charges inside the conductor is also equal to zero at all points (ρ=0).
This can be easily explained with the help of Gauss law
 =0
=0
Example 1.10
A conducting shell of radius R has a charge q uniformly distributed over its surface. Plot a graph following the variation of electric field intensity and electric potential inside and outside the shell.

Solution
Electric field Intensity E Electric potential V
(i) Inside E = 0 (r ≤ R) (i) Inside V = kq/R (r ≤ R)
(ii) Outside E = kq/r2 (r ≥ R) (ii) Outside V = kq/r2 (r ≥ R)
|
Example 1.11 Find the potential of an uncharged conducting sphere provided that a point charge q is located at a distance r from its centre. Solution Since potential V is the same for all points of the sphere. Therefore, we can calculate its value at the centre O of the sphere, because only for this point it can be calculated in the most simple way: V = 1/4πε0 q/r + V' (i) |
 |
where V′ shows the potential of the point O due to induced charges. Since all induced charges are at the same distance R from the point O and the total induced charge is equals to zero, therefore V′= 0
Hence potential of the sphere is given by V = 1/4πε0 q/r
Electrostatic Shielding
If there is a cavity in a conductor or it is hollow, the field strength inside the cavity equals zero whatever is the field outside the conductor. A closed conducting shell divides the entire space into the inner and outer parts which are completely independent of one another in respect of electric fields. This must be interpreted as follows :
|
Any arbitrary displacement of charges inside the shell does not introduce any change in the field of the outer space, and hence the charge distribution on the outer surface of the shell remains unchanged. The same refers to the field inside the cavity (if it contains charges) and to the distribution of charges induced on the cavity walls. This will also remain unchanged upon the displacement of charge outside the shell. |
 |
|
Example : 1.12 A point charge q is within an electrically neutral shell whose outer surface has spherical shape. Find the potential V at the point P lying outside the shell at a distance r from the centre O of the outer surface. Solution The field at the point P is determined only by charges induced on the outer spherical surface since the field of the point charge q and of the charges induced on the inner surface of the sphere is equal to zero everywhere outside the cavity. |
 |
Next, in view of symmetry, the charge on the outer surface of the shell is distributed uniformly, and
hence V = 1/4πε0 q/r.
|
Field Near a conducting Surface The field intensity near a conducting surface is always E = σ/ε0 (1.22) where σ is the local surface charge density at that point Force acting on a conducting surface. The force dF acting on a small element of area dS of the conductor where the local charge density is σ, is given by dF = σ2/2ε0dS |
 |
Example: 1.13
An uncharged metallic sphere of radius r is placed into an external uniform field, as a result of which an induced charge appears on the sphere with surface density σ = σo cosθ, where σo is a positive constant and θ is a polar angle. Find the magnitude of the resultant electric force acting on like charges.
|
Solution According to equation (1.23) the force acting on the area element dS is dF = 1/2 σE dS = σ2dS/2ε0 (i) From symmetry it follows that the resultant force F is directed along the x−axis, and hence it can be represented as the integral of the projections of elementary forces (i) onto the x−axis. |
 |
dFx = dF cosθ
dS = (2π R sinθ) Rdθ = 2π R2 sinθ dθ
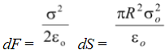 cos2θ sinθ dθ (σ = σo cos θ)
cos2θ sinθ dθ (σ = σo cos θ)
∴ dFx = dF cosθ =  cos3θ sinθ dθ
cos3θ sinθ dθ
On integrating
Fx = 
or Fx =4 
Redistribution of Charge
|
If two conductors are brought into contact, the charges from one of them will flow over to the other until their potentials become equal. The equality of potential implies that charges on each sphere as shown in (fig.1.29) is proportional to its radius i.e. |
|
For a uniform surface charge density σ, the total charge q = 4πR2σ, so the above equation becomes
 (1.24)
(1.24)
The surface charge density of each sphere is inversely proportional to the radius.
Potential of concentric conducting spheres: Superposition Principle
|
Let us consider two spheres of radii r1 and r2 with uniformly distributed charges q1 and q2 as shown in the figure (1.30). Using the principle of superposition, the potential of the small and large sphere may be written as
V1 =
V2 = |
|
|
Example: 1.14 Given two concentric conducting spheres of radii r and R ( r < R) The inner surface carries a charge qo and the outer sphere is earthed. (a) Find the charge on the outer sphere (b) Find the potential of the inner surface |
|
Solution
(a) Let q be the final charge on the outer sphere.
Using equation (1.25 b) the potential of the outer sphere is given by
V2 = 
Since it has been earthed, therefore, V2 = 0
Thus,  = 0 ⇒ q = −qo
= 0 ⇒ q = −qo
(b) The potential of the inner sphere may be obtained using equation (1.25 a)
V1 = 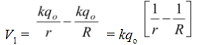
|
Example 1.15 In the previous example if the outer sphere carries a charge +qo and the inner sphere is earthed, then find (a) the charge on the inner sphere, and (b) the potential of the outer sphere. |
 |
Solution
(a) Let q be the charge on the inner sphere.
Using equation (1.25a ) we get
kq/r + kqo/R = 0
Thus q = −qor/R
(b) The potential of the outer sphere is given by equation (1.25 b)
or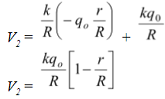

 (1.25 a)
(1.25 a) (1.25 b)
(1.25 b)










