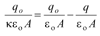Properties of Dielectrics
Electrostatics of Class 12
When a slab of dielectric is inserted to completely fill the space between the plates of a parallel plate capacitor (battery disconnected) as shown in fig. (1.49 b).

The potential difference between the plates decreases by a factor κ, called the dielectric constant.
V = Vo/K
Where Vo is the original potential difference between the plates
Since V = Ed, therefore, electric field also decreases by a factor κ
E = Eo/K
If we insert the dielectric slab to fill the space between the plates without disconnecting the battery, then the potential difference across the plates does not change.

Since the spacing between the plates is also constant, therefore, the electric field intensity between the plates also remain unchanged Vo = Ed
Obviously, the capacitance increases by κ by inserting the slab.
C = κCo
Since q = CVo therefore
q = κCoVo = κqo
Charge on the capacitor increases by a factor κ.
What happens to the energy stored in the capacitor?
(i) Battery disconnected
Initial energy Ui = 
Final energy Uf = 
The energy stored in the capacitor reduces by a factor κ
(ii) Battery connected
Internal energy Ui = 1/2 CoV02
Final energy Uf = 1/2 CV02 = 1/2κCoV02 = κUi
The energy stored in the capacitor increases by a factor κ
The energy density u in the presence of dielectric is given by
u =  (1.36)
(1.36)
Example: 1.20
|
A dielectric slab of thickness h and dielectric constant κ is inserted into a parallel plate capacitor with plates of area A, separated by a distance d, as shown in the figure. The capacitor is charged to a value qo and the battery is disconnected before inserting the slab. (a) Find the capacitance of the capacitor (b) Find the magnitude of the induced charges q |
 |
Solution
(a) The electric field strength in air is
Eo = 
The electric field in the dielectric is
E = Eo/K
The total potential difference between the two plates is
V = Eo (d − h) + Eh = Eo 
Thus, C = 
|
(b) Applying Gauss law for the surface shown in the figure, we have
∴ EA =
or E =
Since E = Using (i) and (ii)
or q = qo (1-1/k) |
|

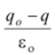
 (i)
(i) (ii)
(ii)