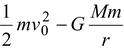Mechanical Energy Of An Orbiting Body

Mechanical Energy Of An Orbiting Body

Consider a satellite of mass m orbiting around earth in a circular orbit of radius r. The total mechanical energy of the system (earth + satellite) is the sum of its potential energy and the kinetic energy of the satellite.

E =

where M is the mass of earth, and v₀ is the orbital velocity of the satellite.

The orbital velocity of a satellite in a stable orbit is given by

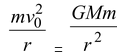
or v₀ = √Gm/r   (11.14)

The kinetic energy is, therefore, given by

K = 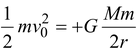     (11.15)

Note that the kinetic energy is half of the magnitude of potential energy.

The total mechanical energy is

E = K + U = −GmM/2R(11.16)

The negative sign of the energy means that the satellite is in a bound state. The quantity |E| is the binding energy of the particle, which is the minimum energy that must be supplied by an external agent to make it an unbound particle − whose mechanical energy is greater than zero.

1. Example 11.2
   1. Find the field strength at a point along the axis of a thin rod of length L and mass M, at a distance d from one end.
   2. 
2. Solution
   1. First we need to find the field due to an element of length dx. The rod must be thin if we are to assume that all points of the element are at the same distance from the field point. The mass of the element is dm = (M/L)dx so contribution to the field is
   2. dg =
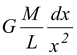
   3. The total field strength is
   4. g =
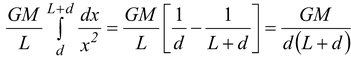
   5. Notice that when d >> L, we find g → GM/d, the result for a point particle.
3. Example 11.3
   1. A rocket with a payload of mass m is at rest at the surface of the earth. Calculate the work needed to raise the payload to the following states:
      1. at rest at an altitude equal to radius of earth (R)
      2. in circular orbit at an altitude R
4. Solution
   1. In both cases the initial energy of the payload is purely potential energy.
   2. E1 = K₁ + U₁= 0 - GmM/R
      1. At the given altitude the distance to the center of the earth is r = 2R.
         1. E₂ = K₂ + U₂ = 0 - GmM/2R
         2. The work needed is E₂ – E₁ = +GmM/R
      2. From equation (11.16), the energy in orbit is
         1. E₃ = K₃+ U₃ = - GmM/4R
         2. The work needed is E₃- E₁ = +3GmM/4R.
5. Naturally, it takes more work to put the satellite into orbit than merely to raise it to the same altitude.