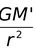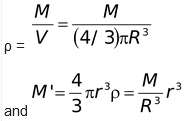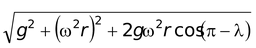The Gravitational Field Strength
Gravitation of Class 11
The Gravitational Field Strength
- Every mass particle is surrounded by a space within which its influence can be felt. This region or space is said to be occupied with gravitational field.
- Each point in the field is associated with a (vector) force which is experienced by a unit mass placed at that point and is called the gravitational field strength.
- If a test mass m at a point in a gravitational field experiences a force F.
-
 (11.4)
(11.4)
|
If the field is produced by a point mass M and the test mass is at a distance r from it then as by Newton’s law of gravitation F = GMm/r2
∴ and is directed towards M. |
|
Field Due to Sphere
- For an external point (r > R) a sphere (solid or hollow) behaves as if whole of its mass is concentrated at its centre, i.e.,
-
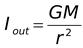 [for r > R](11.6)
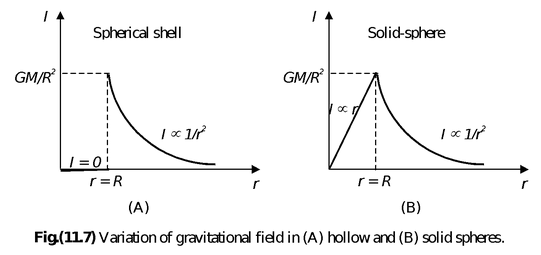
[for r > R](11.6) - In case of a spherical shell, for an internal point, i.e., (r < R) field is zero, i.e.,
- Iin = 0
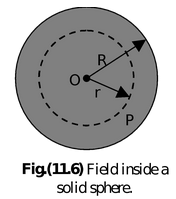
- In case of a spherical volume distribution of mass (i.e., a solid sphere) for an internal point (r < R), the portion of the sphere that lies outside the radius r will not contribute to the field [as the field inside a spherical shell is zero]; so
|
Iin = where M′ = mass of sphere of radius r. Now if M is the mass of solid sphere,
|
|
∴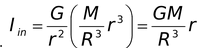 (11.7)
(11.7)
i.e., intensity inside a solid sphere varies linearly with distance from the centre. So it is minimum (Ic = 0) at the centre and maximum at the surface (Is = GM/R2). This is shown graphically in the figure.
Acceleration due to gravity ‘g’
If in Newton’s law of gravitation one body (say earth) is taken as ‘reference body’, the force with which the reference body attracts any other body towards its centre is called force due to gravity (of reference body) and the phenomenon ‘gravity’. Now if the body is free to move, force of gravity (of reference body) in accordance with Newton’s II law will produce an acceleration in it. The acceleration produced in a body by the force of gravity of reference body (usually earth) is called acceleration due to gravity and is represented by ‘g’.
- If the reference body has mass M and radius R, the force on a body of mass m at the surface of reference body by Newton’s law of gravitation will be
- F = (GMm/R2)
- and if ‘g’ is acceleration due to gravity of reference body on its surface, by Newton’s II law,
- F = mg
- ∴g = GM/R2) (11.8)
- This is the relation between g and G and shows that g depends on reference body.
- It is independent of mass, shape, size, etc., of ‘falling body’, i.e., a given reference body produces same acceleration in a light and a heavy falling body.
- Variation in ‘g’
-
With altitude
- As for an external point a spherical distribution of mass behaves as if the whole of its mass were concentrated at the centre, i.e., g = I = (GM/r2)
- so at the surface of earth
- g = (GM/R2)
- and for a height h above the surface of earth
- g′ = [GM/(R + h)2] [as r = R + h]
-
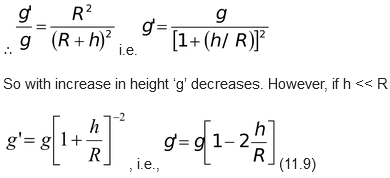
-
With depth
- As in case of spherical distribution of mass for an internal point
- g = I = (GM/R3)r
- So at the surface of earth g = (GM/R2)
- and for a point at a depth d below the surface,
-
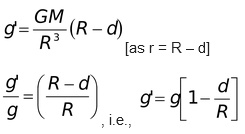
- So with increase in depth below the surface of earth ‘g’ decreases and at the centre of earth it becomes zero.
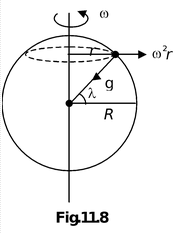
(c) Due to rotation of earthThe earth rotates from west to east on its axis. Every body on the surface of earth experiences a centrifugal force in the reference frame of the earth. The effective value of acceleration due to gravity at a place of latitude λ is given by
g′ = Nowω2r << g |
|
-
∴
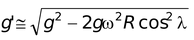 ( r = R cos λ)
( r = R cos λ) - org′ ≈ g - ω2R cos2λ(11.11)
- At equator λ = 0o i.e. g′ ≈ g - ω2R
- At the poles λ = 90o i.e. g′ = g
- Note that the vector g′ is not exactly towards the center of earth.
 (11.5)
(11.5)