De Brogile Waves

de BROGLIE WAVES

The first step in the understanding of the hidden meaning of Bohr's quantum orbits was made by a Frenchman, Louis de Broglie, who tried to draw an analogy between the sets of discrete energy levels that characterise the inner state of atoms and the discrete sets of mechanical vibrations that are observed in the case of violin strings, organ pipes etc.

de Broglie asked himself, 

"Could it not be that the optical properties of atoms are due to some kind of standing waves enclosed within themselves?"

As a result of these considerations, de Broglie came out with his hypothesis that the motion of electron within the atom is associated with a peculiar kind of waves which he called "pilot waves".

In order to have n complete wavelengths (nλ) fit into the circumference of the nth orbit, the following relation must be true:

nλn = 2πrn

From Bohr's theory of the hydrogen atom,

rn   =

or nλn =

or λn   =

The wavelength of the wave associated with a moving particle is equal to Planck's quantum constant divided by the momentum of the particle.

Example  16.6

What is the energy and wavelength of a thermal neutron ? 

Solution

By definition, a thermal neutron is a free neutron in a neutron gas at about 20o C (293 K).

Since it has three degrees of freedom, therefore 

K = J 

λ = = 0.147 nm

Example 16.7

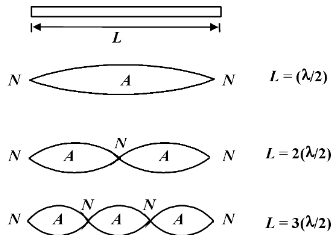
A particle of mass m is confined to a narrow tube of length L. 

(a) Find the wavelengths of the de-Broglie waves which will resonate in the tube,

(b) Calculate the corresponding particle momenta, and 

(c) Calculate the corresponding energies.

Solution

  (a) The de Broglie waves will resonate with a node at each end of the tube.

A few of the possible resonance forms are as follows : 

λn = 2L/n ;  n = 1, 2, 3, ......