Radioactivity
Modern Physics of Class 12
RADIOACTIVITY
Radioactive decay is a random process: Each decay is an independent event, and one cannot tell when a particular nucleus will decay. When a given nucleus decays, it is tranformed another nuclide, which may or may not be radioactive. When there is a very large number of nuclei in a sample, the rate of decay is proportional to the number of nuclei, N, that are present
dN/dt = -λN (16.20)
Where λ is called the decay constant. This equation may be expressed in the form dN/N = -λdt and integrated

to yield

where No is the initial number of parent nuclei at t = 0. The number that survive at time t is therefore
N = Noe-λt (16.21)
This function is plotted in Fig.(16.11)

The time required for the number of parent nuclei to fall to 50% is called the half-life, T, and may be related to λ as follows. Since
0.5 No = No e -λT
we have λT = ln|2| = 0.693. Therefore
T = 0.693/ λ (16.22)
It takes one half-life to drop to 50% of any starting value. The half-life for the decay of the free neutron is 12.8 min. Other half-lives range from about 10-20 s to 1016 years.
Since the number of atoms is not directly measurable, we measure the decay rate or activity (A)
A = - dN/dt. On taking the derivative of equation we find
A = Nλ = λNoe-λt = Roe-λt (16.23)
where A = λN is the initial activity. The activity is characterized by the same half-life. The SI unit for the activity is the becquerel (Bq), but the curie (Ci) is often used in practice.
1 becquerel (Bq) = 1 disintegration per second (dps)
1 curie = 3.7 × 1010 dps
1 rutherford = 106 dps
Mean life of a radioactive sample is defined as the average of the lives of all nucleus.
Tav =  (16.24)
(16.24)
Example 16.10
The half-life of Cobalt - 60 is 5.25 years. How long after its activity have decreased to about one-eigth of its original value ?
Solution
The activity is proportional to the number of undecayed atoms.
In each half-life, half the remaining sample decays.
Since , therefore, three half-lives or 15.75 years are required for the sample to decay to its original strength.
Example 16.11
A count rate-meter is used to measure the activity of a given sample. At one instant the meter shows 4750 counts per minute. Five minutes later it shows 2700 counts per minute.
(a) Find the decay constant
(b) Also, find the half life of the sample
Solution
Initial velocity Ai =  (i)
(i)
Final velocity Af =  (ii)
(ii)
Dividing (i) by (ii), we get
 (iii)
(iii)
The decay constant is given by
λ = 
or λ =  = 0.113 min-1
= 0.113 min-1
Half life of the sample is
T = 
Example 16.12
The mean lives of a radio active substance are 1600 and 400 years for α - emission and
β - emission respectively. Find out the time during which three fourth of a sample will decay if it is decaying both by α - emission and β - emission simultaneously.
Solution
When an substance decays by α and β emission simultaneously, the average disintegration constant λav is given by
λav = λα + λβ
where λα = disintegration constant for α - emission only
λβ = disintegration constant for β - emission only
Mean life is given by Tm = 1/λ
⇒ λav = λα + λβ or  = 3.12 × 10-3
= 3.12 × 10-3
λavt = 2.303 log No/Nt
⇒ (3.12 × 10-3)t = 2.303 log 100/25
⇒ t = 2.303 ×  = 443.5 years
= 443.5 years
There are two types of radioactivity, natural radioactivity observed in unstable elements in nature and artificial radioactivity observed in artificially obtained isotopes.
Example 16.13
The half-life of radium is 1620 years. How many radium atoms decay in 1s in a 1g sample of radium. The atomic weight of radium is 226 kg/mol.
Solution
Number of atoms in 1 g sample is
N = atoms.
The decay constant is
λ =  s1
s1
Taking one year = 3.16 × 107 s
Now,  s-1
s-1
Thus, 3.6 × 1010 nuclei decay in one second.
Natural radioactive processes are of two kinds:
(1) α − decay associated with the emission of α − particles, viz. nuclei 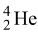 of helium. Alpha particles are heavy positively charged particles having a mass
of helium. Alpha particles are heavy positively charged particles having a mass
mα ≈ 4 amu and a charge qα = +2e. The velocity of α-particles is relatively
low: vα = (c/30 - c /15), where c is the velocity of light.
(2) β−decay (beta-minus-decay) associated with the emission of electrons formed at the instant of decay.
|
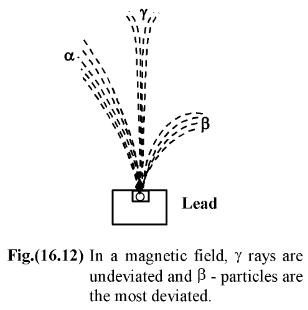
Both processes are accompanied by γ-radiation, i.e. the flow of photons having a very small wavelength, and hence a very high energy. Like other electromagnetic waves, γ-rays propagate at a velocity of light. The penetrability of γ-rays is 0-100 times higher than the penetrability of β-rays and 1000-10000 times higher than the penetrability of In a magnetic field, a beam of α-, β-, and γ-rays splits into three parts. |
|
Nuclei possessing the artificial radioactivity are obtained by bombarding stable nuclei of heavy elements by α-particles, neutrons, or (sometimes) protons and other particles. Nuclear transformations occur in two stages in this case. First a particle hits a target nucleus and causes its transformation into another, unstable (radioactive), nucleus. This newly formed nucleus spontaneously emits a particle and is transformed either into a stable nucleus or into a new radioactive nucleus. Artificial radioactivity obeys the same laws as natural radioactivity.
Radioactive processes occur in accordance with the laws of conservation of energy, momentum, angular conservation, electric charge, and mass number (amount of nucleons).
In α-decay, the mass number of the nucleus decreases by four and the charge decreases by two units, as a result of which two electrons are removed from the atomic shell. The element transforms into another element with the atomic number which is two units lower.
In β--decay, a neutron in the nucleus transforms into a proton. Such a transformation of the neutral neutron into the positive proton is accompanied by the birth of an electron, i.e. by β-radiation. The mass number of the nucleus does not change in this process, while the charge increases by +e and atomic number increases by one.