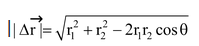Moment of a force (i.e., Torque) about a point
Vector of Class 11
Consider a force acting at point A whose position vector is , then moment of force (i.e, torque) about point O is given by
= (yFz − zFy) + (zFx − xFz) + (xFy − yFx)
|
Physically represents the tendency of the force to rotate the body (on which it acts) about an axis which passes through O and perpendicular to the plane containing the force and position vector . |
|
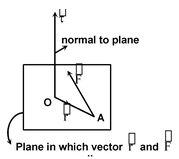
Moment of Force About a Line
Consider a force
acting at a point a whose position vector is
. Then moment of about point O is given by
Then the component of in the direction of vector (i.e., ) is called the moment of force about a line and is given by
= 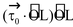
where is unit vector along . In particular if line OL coincides with the x-axis, then
but this is the component of along x-axis
Illustration 18.A force vector 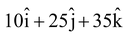 passes through a point (2, 5, 7). Prove that force passes through the origin.
passes through a point (2, 5, 7). Prove that force passes through the origin.
Solution:If the force passes through the origin, its moment about the origin will be zero.
Moment of force (Torque) =
Illustration 19.Determine the torque of the 20 N force (in XY-plane) about point O as shown in figure.
Solution:
= () (20) (5 cos 30°)
= −86.6 Nm
Illustration 20.Find the perpendicular distance from the point (1, 2, 3) to the line joining from the origin to the point (2, 10, 5).
Solution:

perpendicular distance = AB
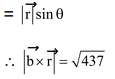
∴AB = 1.84 units
|
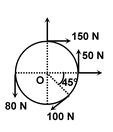
Illustration 21.Determine the resultant of the four forces tangent to the circle of radius 3 m as shown in the figure. What will be its location with respect to the centre of the circle. |
|
Solution:Resolve forces along x and y axis
ΣFx = 150 − 100 cos 45° = 150 − 70.7 = + 79.3 N
ΣFy = 50 − 80 − 100 cos 45° = 50 − 80 − 70.7 = −100.7 N
∴ Resultant force = 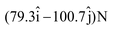
F = 128 N
The torque of 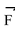 about O is and it equals the sum of the torque of all the given forces about O. Hence
about O is and it equals the sum of the torque of all the given forces about O. Hence
128r = 50(3) – 150(3) + 80(3) − 100(3)
= −360
∴r = 2.81 m
Hence the resultant force of 128 N acts at a distance of 2.81 m form O causing −ve torque.
|
Illustration 22.A cube of side a is acted upon by a force as shown. Find the moment of (a) about point A (b) about the diagonal AG of the cube.
Solution:(a) Moment of about point A is |
|
(b) 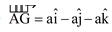
unit vector along 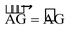 =
=
Moment of about line AG is
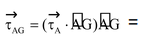
Illustration 23.Two vectors in which one has magnitude twice that of the other, act on a particle. Find the angle between them, if their resultant is perpendicular to the first vector.
Solution:Let the vector  has magnitude twice that of
has magnitude twice that of 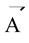 ; |
; |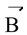 | = 2|
| = 2|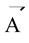 |
|
|
Since
substituting φ = 900 in φ = tan-1
we have |
θ = cos-1 we have θ = 1200. |
|
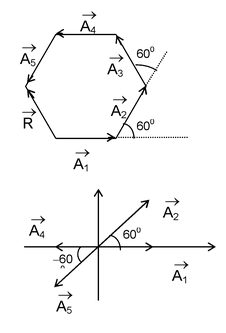
Illustration 24.If five consecutive sides of a regular hexagon represent five unit vectors acting in the same sense, find their resultant vector.
|
Solution:It is relevant from the vector diagram that each vector derivates from its neighbour by an angle of 600. We bring the tails of each vector to a point (origin) and observe that and
|
|
Illustration 25.An insect moves in a circular path of radius R. if it rotates through an angle θ, find its displacement.
|
Solution:When the insect moves from position 1 to position 2, the displacement s = change in position vector
| since the insect moves in a circular path, r1 = r2 = R
Hence | |
|
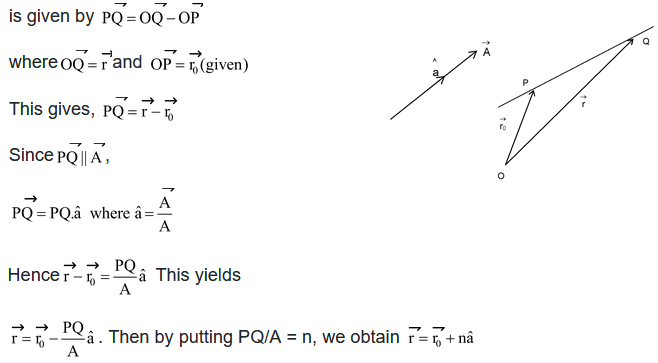
Illustration 26.Find the vector equation of a line which is parallel to a given vector 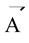 and passes through a given point P having position vector
and passes through a given point P having position vector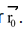 .
.
|
Solution:Let us draw a straight line PQ which is given by |
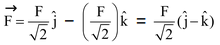

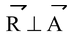 , φ = 900,
, φ = 900,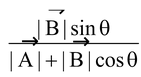
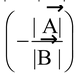 ; substituting |
; substituting |
 are equal and opposite; and
are equal and opposite; and 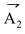 and
and  are equal and opposite.
are equal and opposite.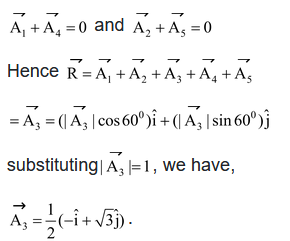
 Since
Since 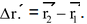 . the magnitude of the displacement is
. the magnitude of the displacement is