Multiplication of vector by a scalar
Vector of Class 11
Let is multiplied by a scalar m. If m is a positive quantity, only magnitude of the vector will change by a factor of ‘m’ and its direction will remain same. If m is a negative quantity the direction of the vector will be reversed, but magnitude of the vector remain same.
Multiplication of Vectors
Vector multiplications are of two types. One, in which we obtain a scalar quantity and the other in which we obtain a vector quantity on multiplication. The first one is called Dot Product and the other is called Cross Product.
(I) Scalar product: cosθ where θ is the angle between the two vectors, when placed tail to tail.
For θ = 900, cos θ = 0 then = 0
Now for orthogonal unit vectors, = 0
Again for θ = 00, cosθ = 1 then = AB
|
For orthogonal unit vectors, =1 Let there be two vectors given by and = AxBx + AyBy + AzBz |
(in the same line) |
Dot product is commutative. i.e.
Angle between two vectors:
As we know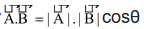
⇒ cos θ
Illustration 13: Two constant forces newton and newton act together on a particle during its displacement from the position m to m. Calculate the work done. If work done by a force, for a displacement is given by.
Solution: Total work done W
= [+]
= 
Illustration 14. Show that if, then the sum and difference of vectors and are at right angles.
Solution:
= 0 (Q )
Illustration 15. If and, find the angle between.
Solution: We have
cos θ =
Where θ is the angle between and
Now . = axbx + ayby + azbz
= 2 × 4 + 3 × 3 + 4 × 2 = 25
Also, a = 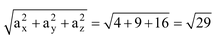
b =
Thus cos θ = or θ = cos-1 ()
(II) Cross product:
The cross product of two vectors inclined to each other by an angle θ is given by
|
If the vectors lie in the x-y plane then the product is perpendicular to the plane i.e. is parallel to z-axis. |
The vector product is not commutative i.e. and
In terms of orthogonal vectors
,
|
If Then, = x In determinant form we have, |
Then, 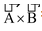 =
=
Cross Product of two parallel or anti parallel vectors is zero.
Note: Division of a vector by a vector is not defined.
Illustration 16. Find the cross product of two vectors and which are
(i) parallel and equal (ii) antiparallel and negative
Solution: If is parallel (or equal) to, θ = 00.
Hence | ×
× 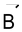 | = AB sin00 = 0
| = AB sin00 = 0
If is antiparallel (or negative) to, θ = 1800. Hence
| 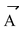 ×
×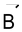 | = AB sin1800 = 0
| = AB sin1800 = 0
If is perpendicular to, θ = 900
Then = |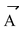 ×
×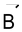 | = AB sin900 = AB and C(=×) is directed outwad obeying right hand thrum rule. × must be perpendicular to the plane containing and.
| = AB sin900 = AB and C(=×) is directed outwad obeying right hand thrum rule. × must be perpendicular to the plane containing and.

Illustration 17. If the magnitudes of the dot product and cross product of two vectors are equal, find the angle between the two vectors.
Solution: |
A.B sinθ = A.B cosθ ⇒ tanθ = 1
⇒ θ = 450.
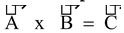 , a vector. where =
, a vector. where =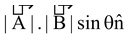 , where is the unit vector along a direction which is perpendicular to plane containing &. Its direction is given by the right hand thumb rule, or right hand screw rule. || gives the area of the parallelogram, formed by and
, where is the unit vector along a direction which is perpendicular to plane containing &. Its direction is given by the right hand thumb rule, or right hand screw rule. || gives the area of the parallelogram, formed by and 








