Some important properties of binomial theorem

(a) The number of terms in the expansion of (x + y)n is (n + 1).

(b) General term = (r + 1)th term

⇒ T^r+1 == ⁿCrx^n-ryr, r = 0, 1, 2, …….n.

(c) Middle term

It depends on the nature of n

• If n is even then the number of terms being (n + 1) is odd, therefore there is only one middle term i.e. 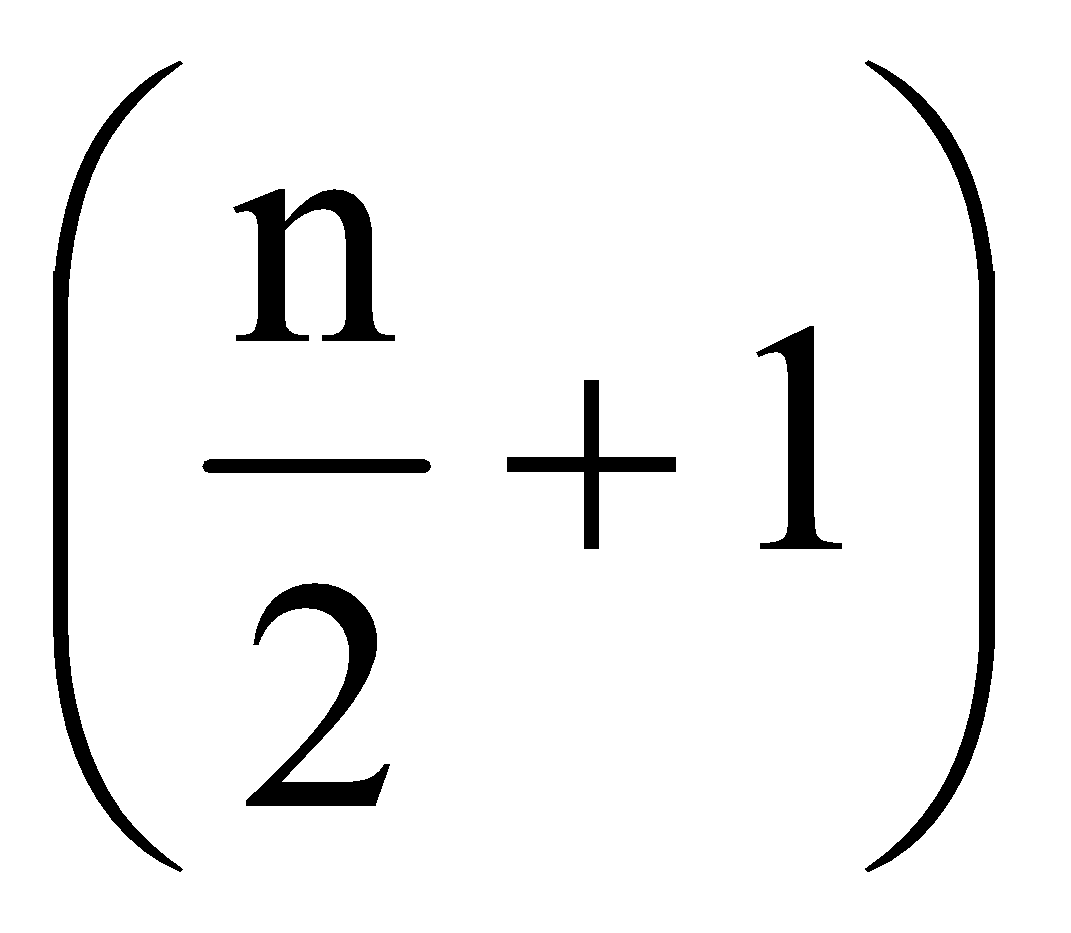th term.
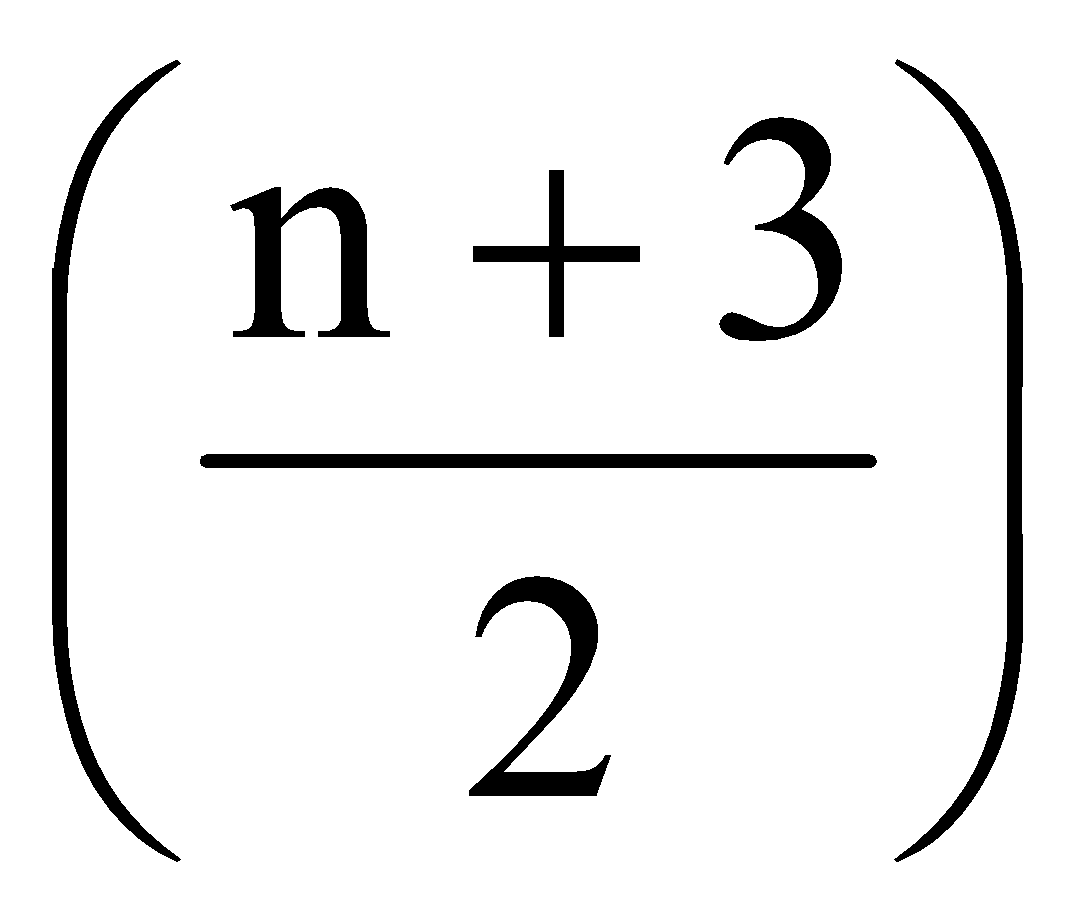• If n is odd, then total number of terms in the expansion is even. So there are two middle terms is th term and th term.

(d) To find (p + 1)th term from the end It is equal to ( n – p + 1)th term from the beginning

i.e. Tn – p + 1 = ⁿC_n – p x^n-pyp

(e) Greatest term

To find the greatest term numerically in the expansion of (1 + x)n

• calculate p =
• if p is integer, then Tp and TP+1 are equal and both are greatest terms.
• if p is not an integer then T[p] + 1 is the greatest term, where [p] is the greatst integer not greater than p.

(f) How to find greatest term in the expansion of (x + y)ⁿ

We have

(x + y)ⁿ = xⁿ(1 + )ⁿ

then find the greatest term in the expansion of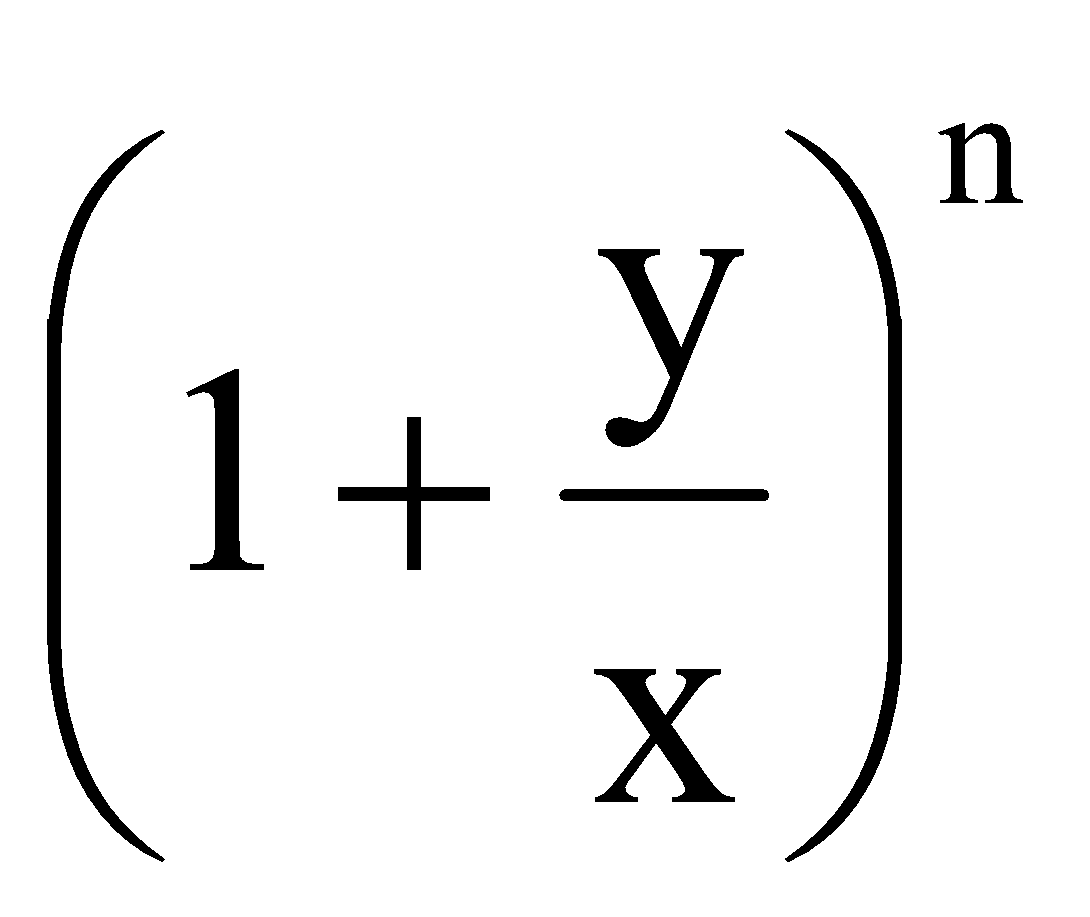

(g) Greatest Coefficient

• If n is even then the greatest coefficient is ⁿC_n/2. 
• If n is odd then they are 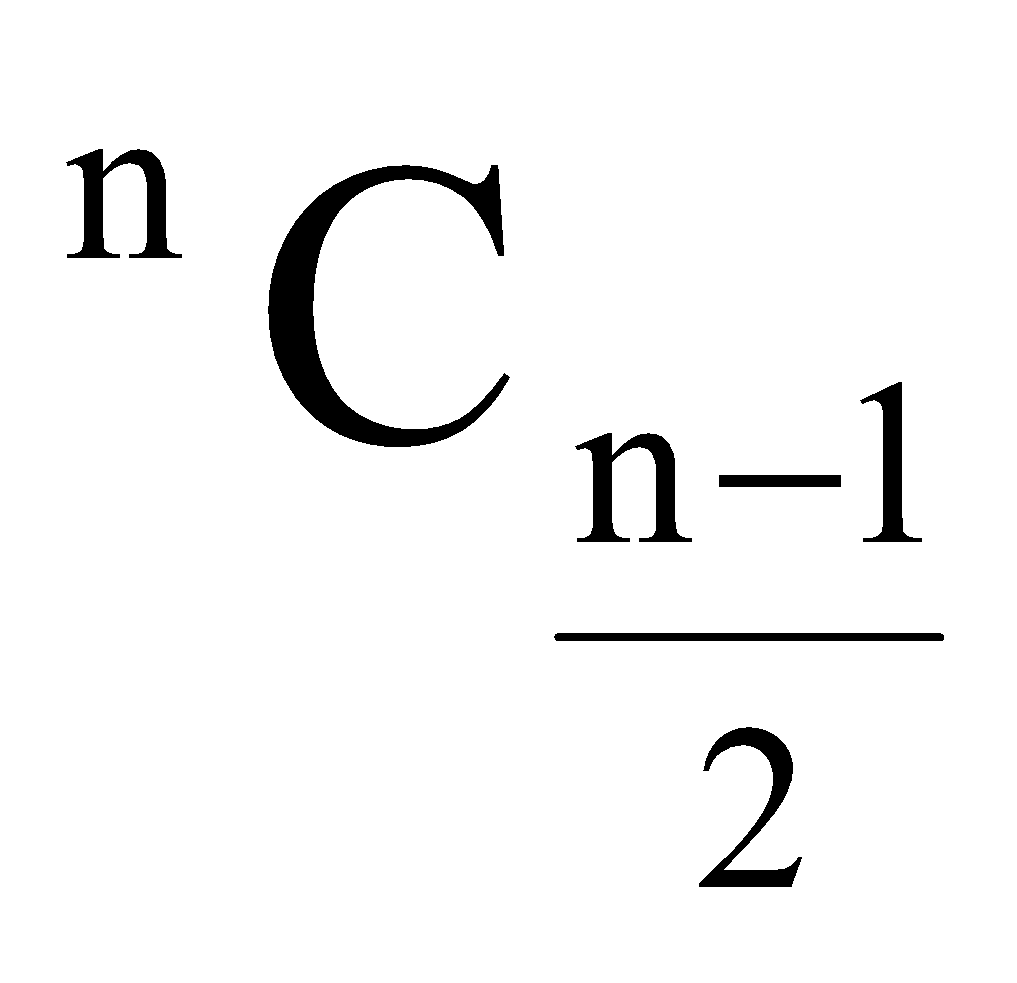, and 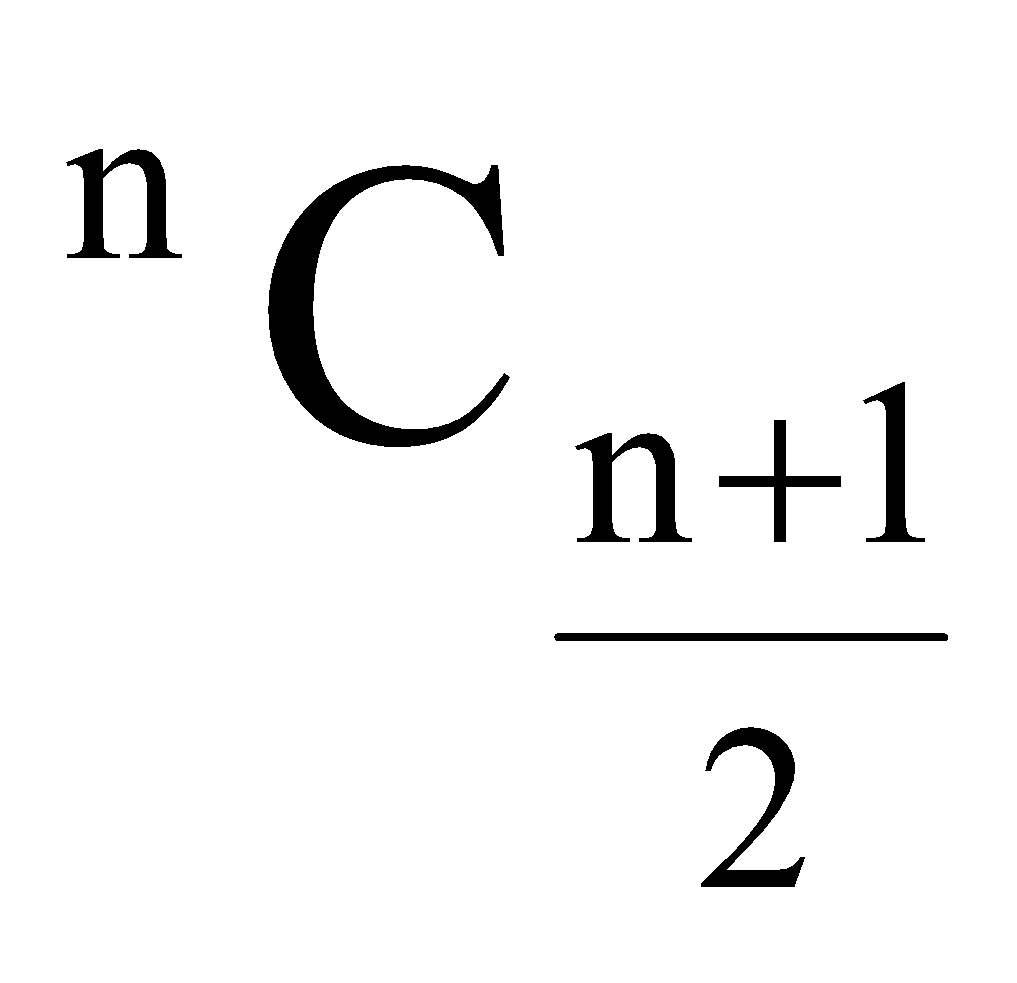.