Definition of a Determinant

Definition of a Determinant

A determinant is an arrangement of n × n numbers into n − horizontal lines (each line is called a row) and n vertical lines (each line is called a column) enclosed into two vertical bars. It is denoted by D or Δ.

A determinant having n × n numbers is called determinant of order n.

The number aij which appears in the ith row and jth column is called (ij)th entry of the determinant.

Diagonal Elements

The entries 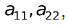 … , ann are called diagonal entries and all other entries are called non-diagonal entries.

Minor

To each entry of a determinant we associate a number (uniquely determined) called its minor. The minor of aij, denoted by M_ij, is the determinant, which is obtained on deleting ith row and jth column from the original determinant.

Note: The value of M_ij is independent of the value of a_ij.

Cofactor

Again to each entry of a determinant we associate a number (uniquely determined) called its cofactor. The cofactor of aij, denoted by Cij, is defined by

C_ij = (−1)i + j M_ij