Some More Special Type of Matrices

Some More Special Type of Matrices

(i) Symmetric Matrix

A matrix A = [a_ij] n×n is symmetric if A = A′. Note that aij = aji for such a matrix, ∀ 1 ≤ i, j ≤ n.

(ii) Skew Symmetric Matrix

A matrix A = [aij]n×n is skew symmetric if A = – A′. Note that a_ij = –a_ji for such a matrix, ∀ 1 ≤ i, i ≤ n. If i = j, then aii = –a_ii  ⇒ a_ii = 0. Thus in a skew symmetric matrix diagonal entries are zeros.

Note that every square matrix can be written (uniquely) as the sum of a symmetric and a skew symmetric matrix, i.e., A = .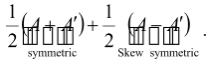

(iii) Hermitian Matrix

A matrix A = [aij]n×n is hermitian if A* = A. Note that aij = ji for such a matix. Thus in a skew hermitian matrix aii = ii ⇒ diagonal entries of a hermitian matrix are real.

(iv) Skew Hermitian Matrix

A matrix A = [aij]n×n is skew hermitian if A* = –A.

Note that aij = –_ji. Thus in a hermitian matrix aii = –_ii ⇒ diagonal entries of a skew hermitian matrix are either zero or purely imaginary.

Note that every square matrix can be written (uniquely) as the sum of a hermitian and a skew–hermitian matrix i.e., .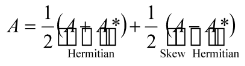

(v) Orthogonal Matrix

A matrix A = [a_ij]_n×n is orthogonal if AA′ = In. Thus in a 3 × 3 orthogonal matrix rows (columns) are forming orthogonal system of unit vectors and vice versa. For example 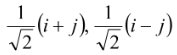and are forming orthogonal system of unit vectors. The corresponding matrix is .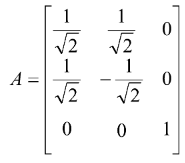

Note that AA′ = I3. Thus A is an orthogonal matrix.

(vi) Unitary Matrix

A matrix A = [a_ij]_n×n is unitary if AA* = In. For example the matrix is unitary.