Inverse of a Square Matrix

Inverse of a Square Matrix

Let A be any n − rowed square matrix. Then a matrix B, if exists, such that AB = BA = In, is called the inverse of A. Inverse of A is usually denoted by A–1 (if exists). We have
|A| In = A(adj_A) ⇒ |A| A–1 = (adj_A). Thus the necessary and sufficient condition for a square matrix A to possess the inverse is that |A| ≠ 0 and then A−1 = 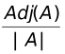. A square matrix A is called non–singular if |A| ≠ 0 . Hence a square matrix A is invertible if and only if A is non–singular.