Multiplication of Matrices
Matrices and Determinants of Class 12
Multiplication of Matrices
Let A = [aij]m × n and B = [bjk]n × p be two matrices such that the number of columns in A is equal to the number of rows in B. Then the m × p matrix C = [Cik]m×p,
where Cik =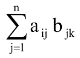 
, is called the product of the matrices A and B in that order and we write
C = AB.
- Definition of a Matrix
- Special Types of Matrices
- Equality of Two Matrices
- Addition of Matrices
- Multiplication of Matrices
- Properties of Matrix Multiplication
- Transpose of a Matrix
- Transposed Conjugate of a Matrix
- Properties of Transpose and Conjugate Transpose of a Matrix
- Some More Special Type of Matrices
- Adjoint Of A Square Matrix
- Inverse of a Square Matrix
- Definition of a Determinant
- Value of a Determinant
- Properties of Determinants
- System of Linear Simultaneous Equations
- System of Linear Non Homogenous Simultaneous Equations
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
