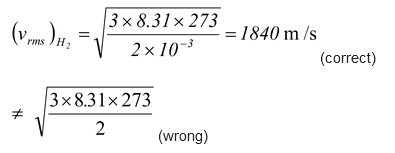Kinetic Theory

Kinetic theory attempts to provide insight into the underlying microscopic basis for the macroscopically observed behavior of gases. In kinetic theory, a gas is assumed to consist of a very large number of molecules that move about randomly and collide frequently. At atmospheric pressure and room temperature, 1 cm3 of gas consists of approximately 3 × 10¹⁹ molecules. Although one cannot apply Newton’s laws to each molecule, one can relate the average value of certain quantities at the macroscopic level of quantities, such as pressure and temperature, that are observable at the macroscopic level.

THE MODEL OF AN IDEAL GAS

In the kinetic theory of gases, the following assumptions are made about the molecules
of a gas:

1. The gas consists of a very large number of identical molecules moving with random velocities.

2. The molecules have no internal structure, so all their kinetic energy is purely translational. (We will later incorporate the possibility of rotation or vibration of a molecule)

3. The molecules do not interact except during brief elastic collisions with each other and with the walls of the container. This means that they exert strong repulsive forces only at close range. The duration of each collision is much shorter than the time between collisions, so the potential energy associated with these forces is negligible.

4. The average distance between the molecules is much greater than their diameters. This means that they occupy a negligible fraction of the volume of the container. (From the incompressibility of liquids, we can infer that the molecules in a liquid are nearly as close together as possible. Since the density of the gas is about 10-3 of the density of the liquid, the assumption that the molecules are far apart is reasonable. The average separation between molecules in a gas is about 10 atomic diameters at atmospheric pressure and room temperature.)

Kinetic Interpretation of Pressure

Consider a gas confined to a cube of side L, as in figure(5.4). We wish to calculate the pressure exerted on a face perpendicular to the x-axis. To simplify matters, we assume initially that the molecules do not collide with each other. We focus our attention on one molecule whose velocity has the x component v1x. When it collides elastically with the wall, as in figure, the y and z components of its velocity are unchanged, whereas the x component merely reverses its direction. The change in linear momentum of the molecule is

Δpx = (-mv₁x) – (mv₁x) = -2mv₁x

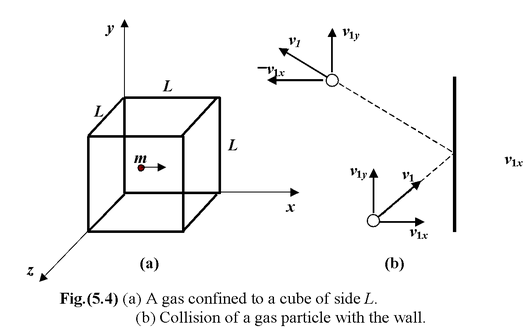
The wall experiences an equal and opposite impulse. The molecule will strike the opposite wall and return after a time interval Δt = 2L/v1x.

A single molecule therefore exerts a series of impulses on the wall. The (time) average force exerted by this one molecule is

F1 =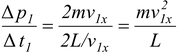

The total average force exerted by all the molecules is the sum

F = 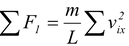(5.3)

We cannot find 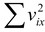since we do not know how the velocities of the molecules are distributed. However, we note that the average value of vx2 taken over all the N molecules in the gas (not the average for any single molecule) is

The speed of ith molecule is given by 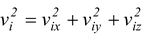, so the average taken over all the molecules is

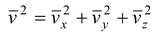
Since the motion of the molecules is completely random, there is no preferred direction. Thus, one would expect that

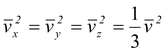
Using 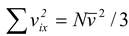in equation no. (5.3) , we find that the total average force is

F =

and the pressure, P = F/A exerted on the wall of area A = L2, is

P = (5.4)

where V = L3

The root mean square (rms) speed of the molecules is defined as

vrms = 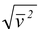(5.5)

In terms of the mass density, ρ = Nm/V, equation (5.4) becomes

P = 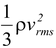(5.6)

This equation is important because the macroscopic variable pressure is expressed in terms of the rms speed of the molecules, a microscopic variable.

Although this result has been derived for a cubic box, it does not depend on the shape of the container. Although collisions between pairs of molecules lead to the exchange of linear momentum between them, the force exerted on a wall averaged over all the molecules is not affected.

Example: 5.4

The speeds (in m/s) for 8 molecules are 2, 4, 5, 5, 8, 9, 11 and 15. Find

(a)their average speed

(b)their rms speed

Solution

(a)The average speed is given by

vav = 1/N (v1 + v2 + ………..+ vN)

= (2 + 4 + 5 + 5 + 8 + 9 + 12 + 15)/8 m/s

= 7.5 m/s

(b)To find the rms speed we first find the average of v2:

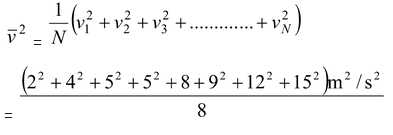
= 73 m²/s²

Then, vrms= 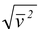8.54 m/s

In general the average speed is not equal to the rms speed.

Example: 5.5

In a certain region of space there are only 5 molecules per cm3 on an average. The temperature is 3 K. What is the average pressure of this very dilute gas?

(k = 1.38 × 10^-23 J/mol K)

Solution

According to ideal gas equation PV = nRT,

or P = (nNAkT/V)[as R = NAk]

Also the number of molecules N = nNA

∴PV = NkT

or P = N/V kT where N/V is the number of molecules per unit volume.

Here N/V= 5 molecules/cm3 = 5 molecules/(10^-2 m⁾³ = 5 × 10⁶ molecules/m3

Thus P = (5 × 10⁶)(1.38 × 10^-23)(3) = 2.07 × 10^-16 Pa

Kinetic Interpretation of Temperature

From the point of view of kinetic theory, temperature is a quantity characterizing the average kinetic energy of translatory motion of the molecules of an ideal gas.

Equation (5.21) may be written in the form,

PV =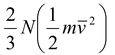

Comparing the above equation with PV = NkT, we can find the average kinetic energy of a molecule as

Kav = (5.7)

For an ideal gas, the absolute temperature is a measure of the average translational kinetic energy of the molecules.

Note that the kinetic energy in equation (5.7), is associated with the random translational motion of a single molecule.

It does not include any orderly motion imposed.

The rms speed of molecules varies with temperature as

vrms = √3kT/m

In terms of molar mass M (kg/mol), the rms speed is given by

vrms = √3RT/M (5.8)

Example: 5.6

Find the average translational kinetic energy of molecules in air at 300 K.

Solution

Although air consists of a mixture of gases, they all have the same average translational kinetic energy.

Kav = 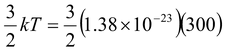= 6.21 × 10-21 J

Example: 5.7

Calculate the root mean square speed of smoke particles of mass 5 × 10-17 kg in their Brownian motion in air at NTP (k = 1.38 × 10-23 J/K).

Solution

According to kinetic theory of gases

vrms = 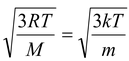(as R = NAk and M = NAm)

HereT = 273 K, m = 5 × 10-17 kg and k = 1.38 × 10-23 J/K

so vrms = = 1.5 × 10-2 m/s = 1.5 cm/s

Example: 5.8

Two vessels having equal volume contain molecular hydrogen at one atmosphere and helium at two atmospheres respectively. What is the ratio of rms speed of hydrogen molecule to that of helium molecule, assume that both the samples are at the same temperature?

Solution

According to kinetic theory of gases,

vrms =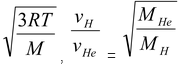

vH =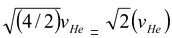

Note If one uses the relation vrms =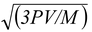

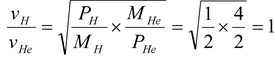i.e.vH = vHe

This solution is wrong as in it M is not molecular weight but total mass of gas. Now as pressure of helium is double that of hydrogen at same temperature and volume, in accordance with Avagadro’s law the number of moles of helium will be double that of hydrogen.

so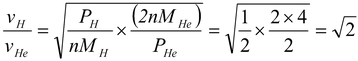

Example:5.9

At what temperature will the rms speed of oxygen molecule will be sufficient for escaping from the earth?

(ve = 11.2 km/s, m = 2.76 × 10^-26 kg and k = 1.38 × 10^-23 J/K)

Solution

If the temperature is T, according to kinetic theory of gases

translational KE = (3/2)kT

The oxygen molecule will escape from earth if

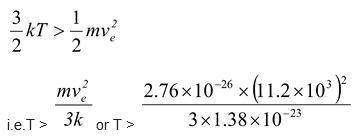
i.e.T > 8.36 × 104 K

Different Speeds of Gas Molecules

The motion of molecules in a gas is characterized by any of the following three speeds.

(a) Root mean square speed

It is defined as the square root of mean of squares of speed of different molecules, i.e.

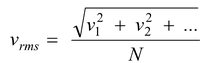
and according to kinetic theory of gases

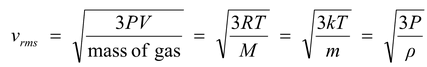(5.9)

where M is molecular mass and m is the mass of a single molecule and ρ is the density of gas.

k = Boltzmann constant

= R/Avogardo Number

= 1.38 × 10−23 J/mol.K

(b) Most probable speed

It is the speed, which is possessed by maximum number of molecules in a gas at constant temperature.

(5.10)

(c) Average speed

It is the arithmetic mean of the speeds of molecules in a gas at a given temperature. i.e.

v_av =

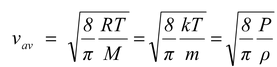(5.11)

Important

(i)vrms > vav > vmp(R A M)

One can easily remember the above relation by remembering the word RAM where

R stands for rms

A for average

M for most probable

and vrms : vav : vmp = √3 : √8/π : √2 (5.12)

since 8/π ≈ 2.5

∴vrms : vav : vmp = √3 : √2.5 : √2

(ii)Speed of sound in a gas =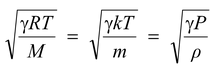

i.e., the speed of sound in a gas is of the same order as rms speed of its molecules.

In a nutshell we can write

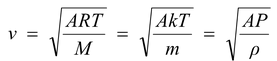
where A is a number whose value is given by

A = 3 for v_rms

= 8/π  for v_av

= 2 for v_mp

= γ for v_sound

Note that in the above expression the molecular mass M should be taken in kilogram (not in gram)

For example, at NTP the rms speed of hydrogen gas is given by