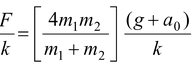Reference Frames: Inertial And Non−Inertial
Share
Reference Frames: Inertial And Non−Inertial
Laws Of Motion of Class 11
A reference frame in which Newton’s first law is valid is called an inertial reference frame. In an inertial reference frame, a body subject to no net force will either stay at rest or move at constant velocity.
Any frame moving at constant velocity relative to a known inertial frame is also an inertial frame. If the acceleration of a particle is zero in one inertial frame, it is zero in all inertial frames.
An accelerated frame of reference is called a non−inertial frame. Objects in non−inertial reference frames do not obey Newton’s first law.
Suppose a ball is on the frictionless floor of a car and the brakes are applied. Since there is no net force on the ball an observer on the ground will see the ball continue to move at the velocity of the car just before the brakes were applied. However, relative to an observer in the car, the ball accelerates in the forward direction, even though there is no net force on it. To explain the acceleration of the ball with respect to the car (non−inertial frame) one has to invent a fictitious force called the pseudo force. It is an imaginary force which acts on all the occupants of an accelerated frame. The direction of the force is opposite to the direction of the acceleration.
FP = −ma
This pseudo force is real enough to throw you forward when a bus suddenly stops. It is fictitious in the sense that it has no physical origin, that is, it is not caused by one of the basic interactions in nature. Its action does not have the reaction required by the third law.
|
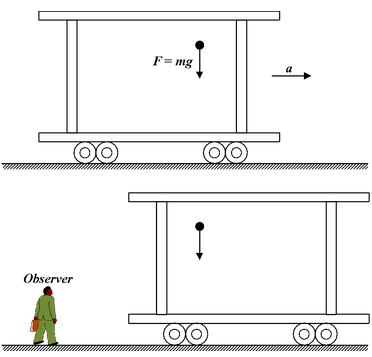
Fig.(6.17) (a) A ball is dropped inside a car which is initially at rest but has an acceleration a to the right A person on the ground observes that the ball is falling vertically downward under gravity. |
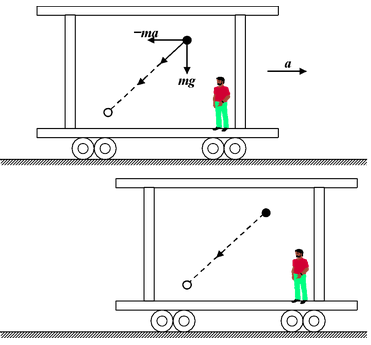
Fig.(6.17)(b) A person in the accelerated car observes that the ball falls down and towards the left of the car. According to him the backward acceleration is caused by the pseudo force. |
Example 6.9
|
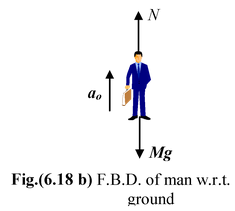
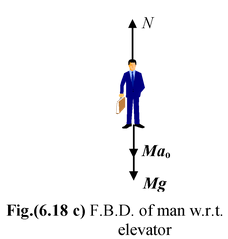
Apparent weight in an Accelerating Elevator : A man of mass M stands on a scale in an elevator, as shown in the figure. Find the scale reading when the elevator is accelerating with a0. (i) upward and (ii) downward ? Solution (a)Since the man is stationary relative to the elevator, it is also accelerating up with a0. The forces on the man are reaction N (exerted by the scale platform on which it rests) and Mg, the force of gravity. In the reference frame attached to the elevator an additional pseudo force FP = Ma0 acts opposite to the acceleration. The free body diagrams of the man w.r.t. ground and the elevator are shown in Fig.(6.18 b & c). |
|
|
Applying Newton’s Second Law N – Mg = Mao orN = M(g + ao) |
N – Mg – Mao = 0 orN = M(g + ao) |
The force exerted by the man on the scale is equal and opposite to N and determines the reading on the scale or the apparent weight. Thus, when the elevator accelerates up, the apparent weight of the block is greater than its true weight by Ma0.
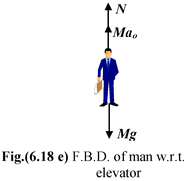
(b)When the elevator accelerates downward with a0 the free body diagrams can be drawn as shown in the figure.
|
Applying Newton’s Second Law Mg – N = Mao orN = M(g – ao) |
with respect to the elevator N + Mao – Mg = 0 orN = M(g – ao) |
Thus, when the elevator accelerates down, the apparent weight of the man is lesser than his true weight by Ma0.
If a0 = g, as it would if the elevator were in free fall, the man would be apparently weightless.
|
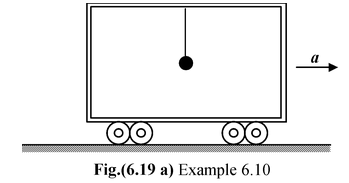
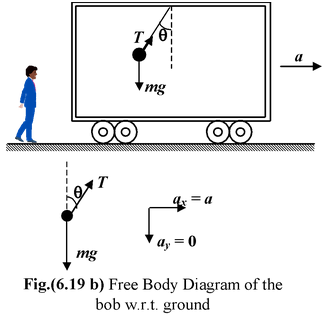
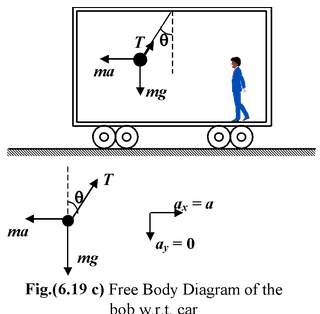
Example: 6.10 Figure shows a pendulum suspended from the roof of a car that has a constant acceleration a relative to the ground. Find the deflection of the pendulum from the vertical as observed from the ground frame and from the frame attached with the car. |
|
Solution
|
In an inertial frame the suspended bob has an acceleration a caused by the horizontal component of the tension T. T sin θ = ma..(i) T cos θ - mg = 0 ..(ii) From equation (i) and (ii) tan θ = a/g orθ = tan−1(a/g) |
In the non−inertial frame of the car, the bob is in static equilibrium under the action of three forces: T, mg and ma T sin θ = ma..(iii) T cos θ = mg..(iv) From equation (iii) and (iv) tan θ = a/g orθ = tan−1(a/g) |
|
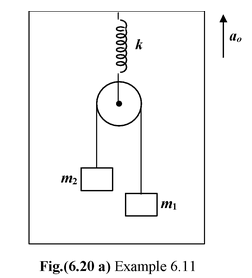
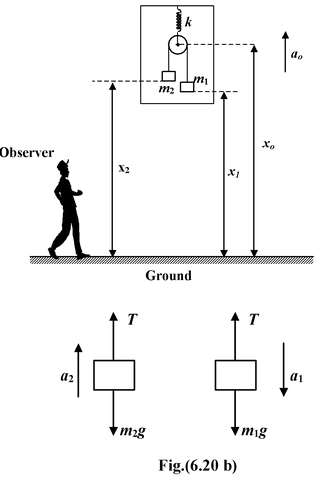
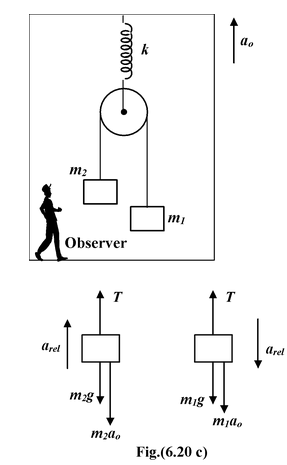
Example: 6.11 A pulley with two blocks system is attached to the ceiling of a lift moving upward with an acceleration a0. Find the deformation in the spring as observed by the inertial and non−inertial reference frame observer. |
|
Solution
Inertial Frame
|
Non - Inertial Frame
|
Applying Newton’s Second Lawm1g − T = m1a1(i) −m2g + T = m2a2(ii) Constraint relation (x0 − x2) + (x0 −x1) = constant or 2x0 − x1 −x2 = constant Differentiating twice w.r.t. time we get
2 or 2a0 − (−a1) − a2 = 0 or a2 = 2a0 + a1(iii) |
Relative to the centre of the pulley m1 accelerates downward with arel and m2 accelerates upward with arel. Applying Newton’s Second Law m1g + m1a0 − T = m1arel(iv) −m2g − m2a0 + T = m2arel(v) On adding equations
arel = Substituting arel in equation (iv)
T = |
|
Solving equations (i), (ii) and (iii),
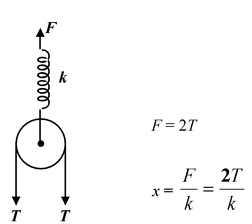
we get T= The stretching force on the spring is F = 2T Using Hooke’s law F = kx where x is the deformation in the spring.
Thus, x = |
|
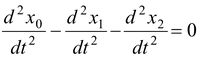
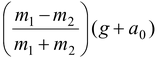
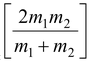(g + a0)
