AVOGADRO’S LAW
States of matter of Class 9
AVOGADRO’S LAW
In 1812, Amadeo Avogadro stated that samples of different gases which contain the same number of molecules occupy the same volume at the same temperature and pressure. It follows from Avogadro's hypothesis that V ∝ n (when T and P are constant)
.png) = Constant or
= Constant or 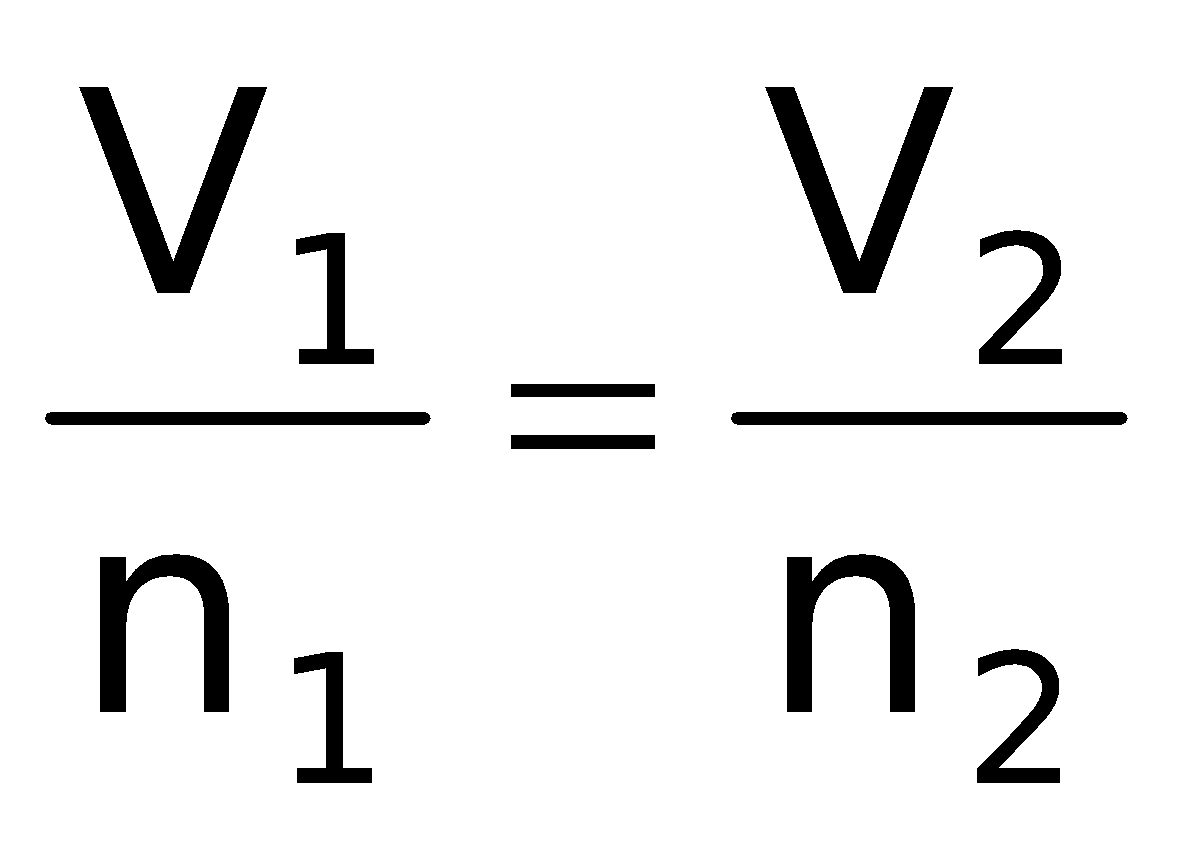
Combined gas equation:
The equation, which gives relationship between the three measurable variables P, V and T of a gas is called combined gas equation.
Applying Boyle’s law, we can write,
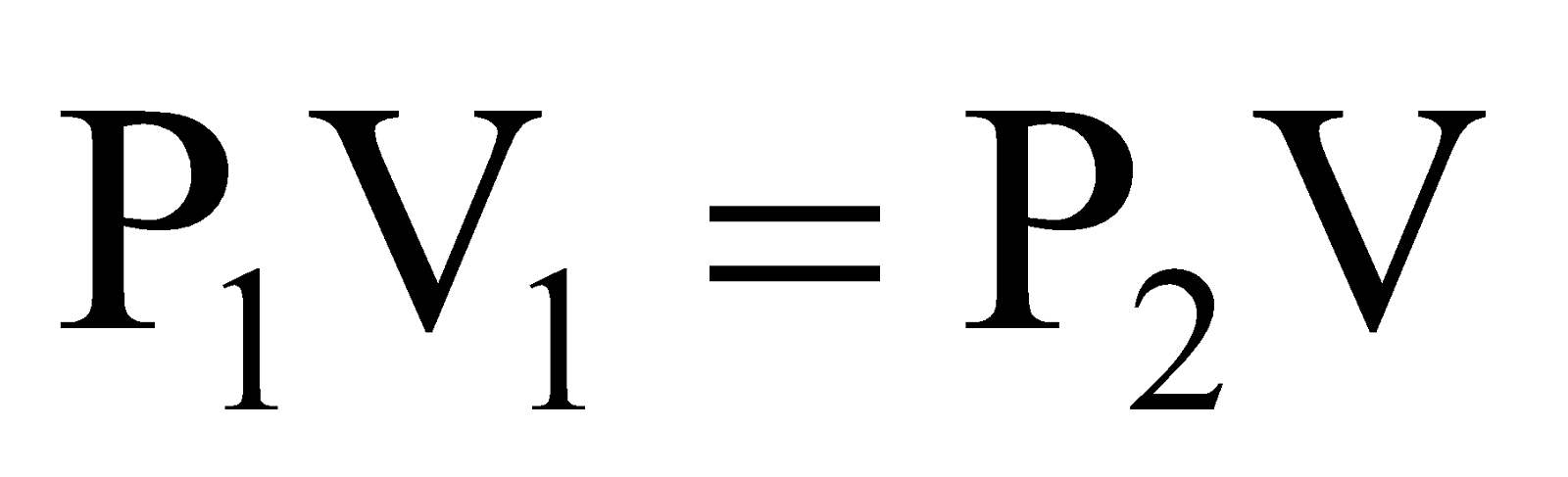 or
or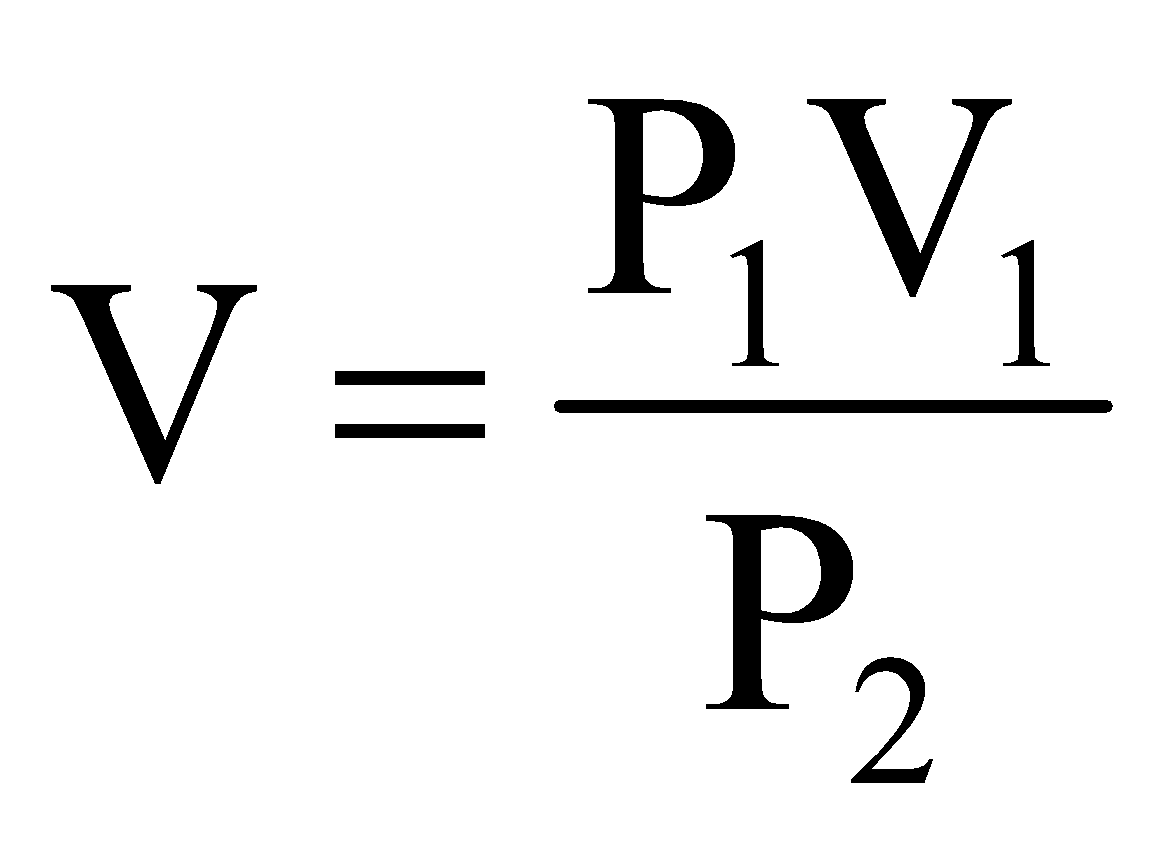 ..... (i)
..... (i)
Applying Charle’s law we can write,
 ..... (ii)
..... (ii)
Comparing equation (i) with equation (ii), we get,
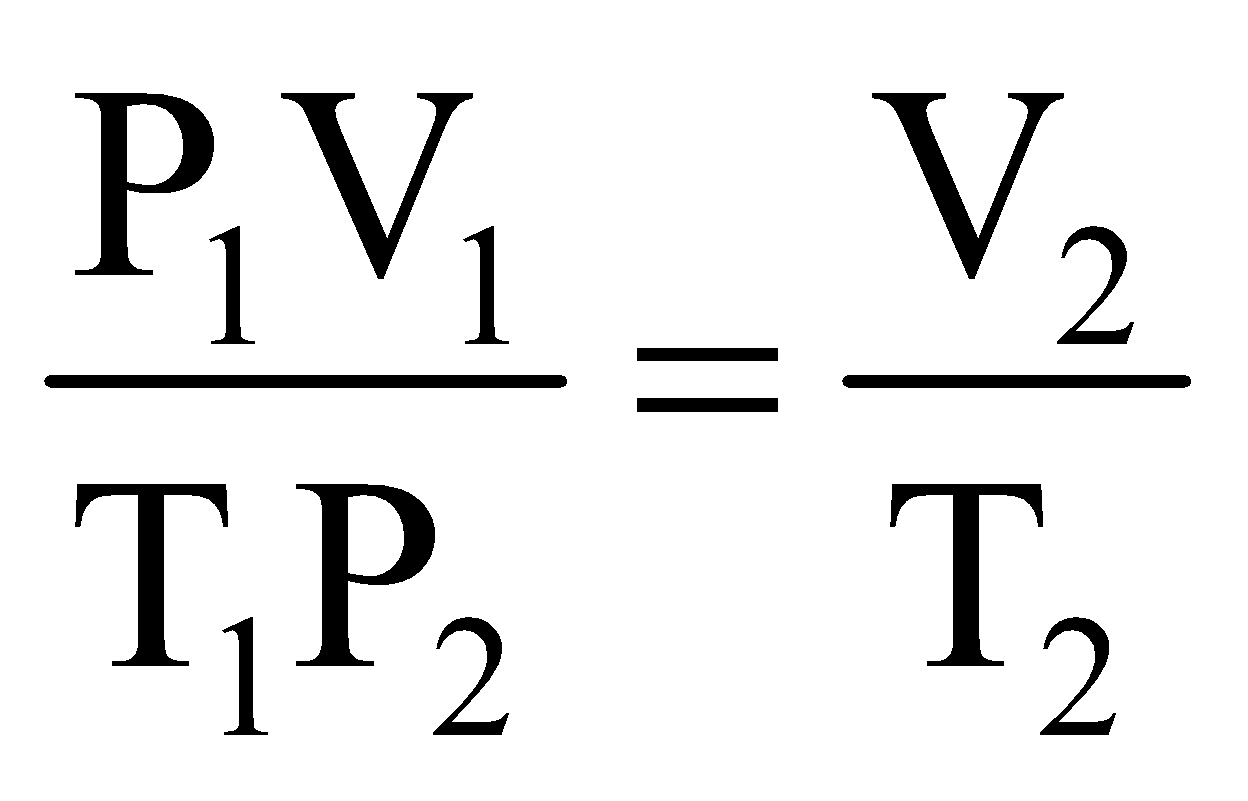
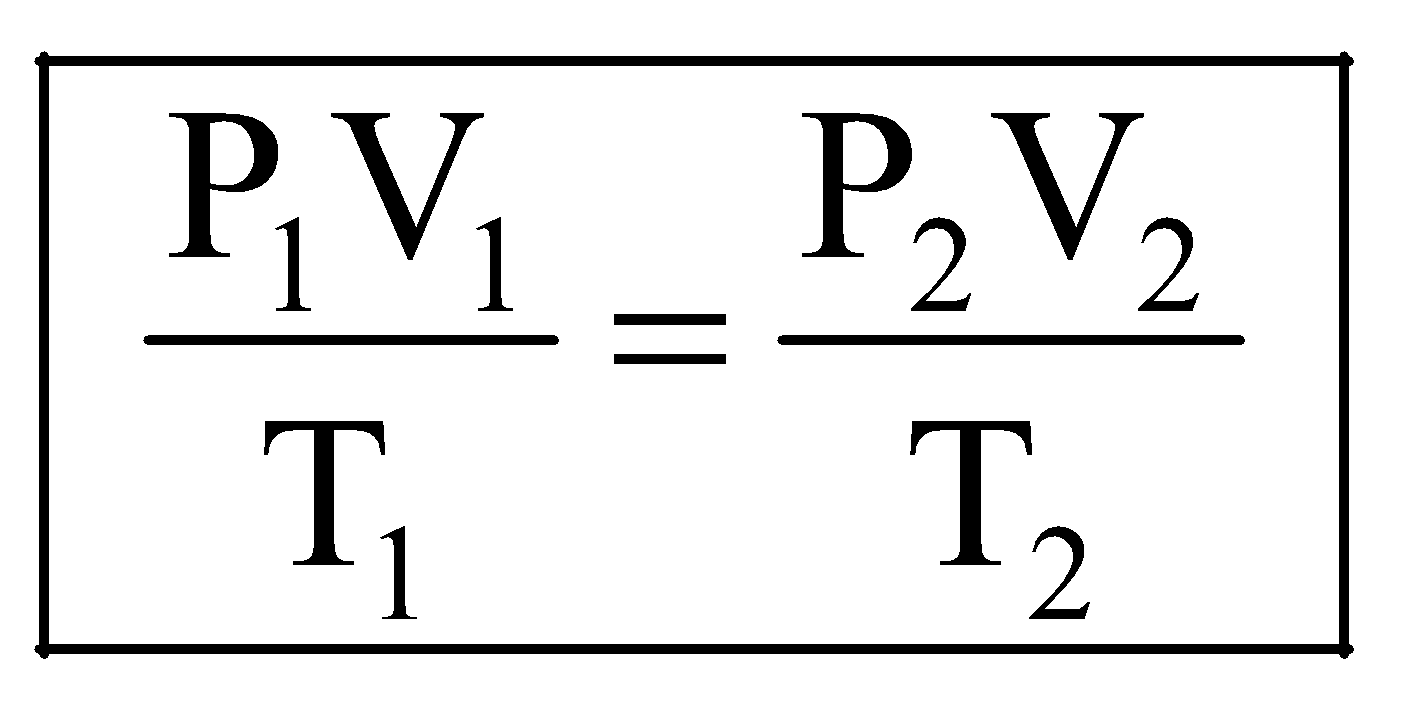 .
.
This is known as combined gas equation.
Example 4 .Calculate the temperature at which volume of a gas at 2 atm will be twice its volume at S.T.P.
Solution: Let volume of gas at S.T.P. is V, then volume under given condition will be 2 V. Applying combined gas equation we get,
(S.T.P. condition) 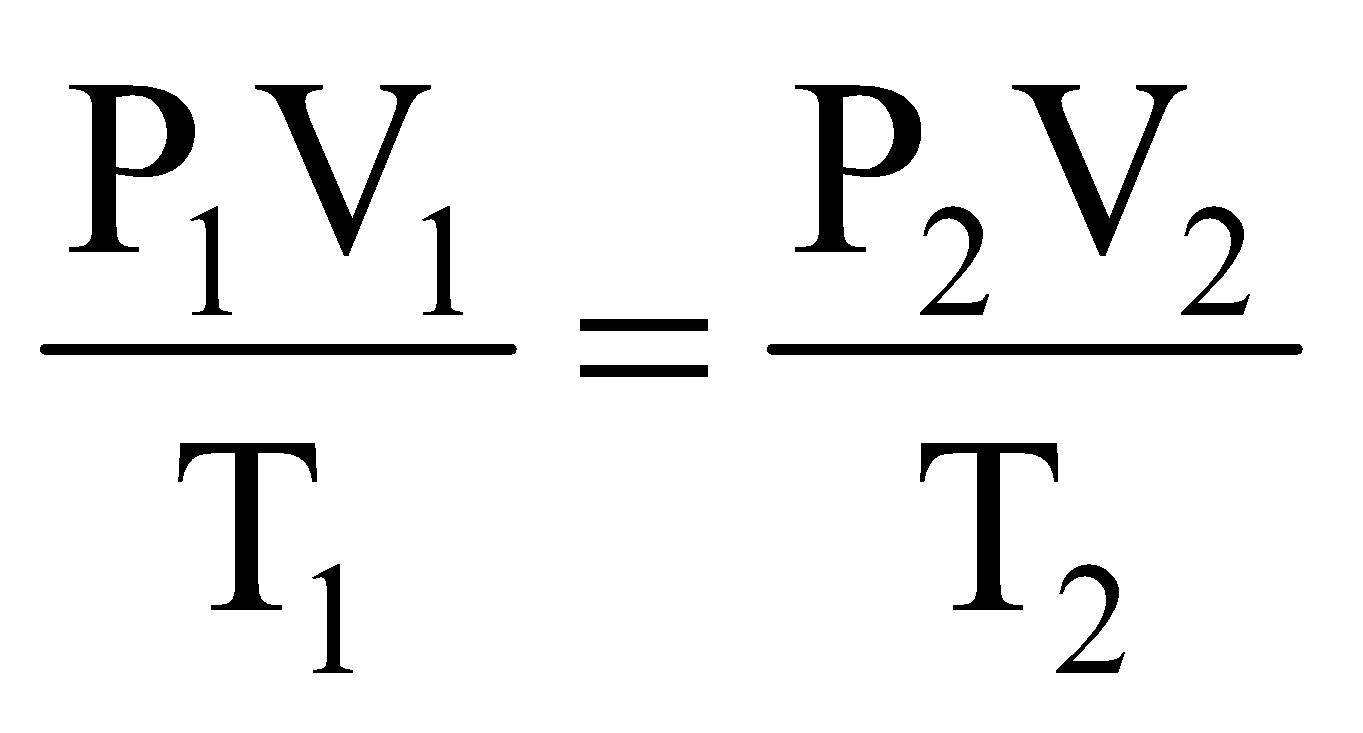 (Given condition)
(Given condition)
Here, P1 = 1 atm V1 = V T1 = 273 K
P2 = 2 atm V2 = 2 V T2= ?
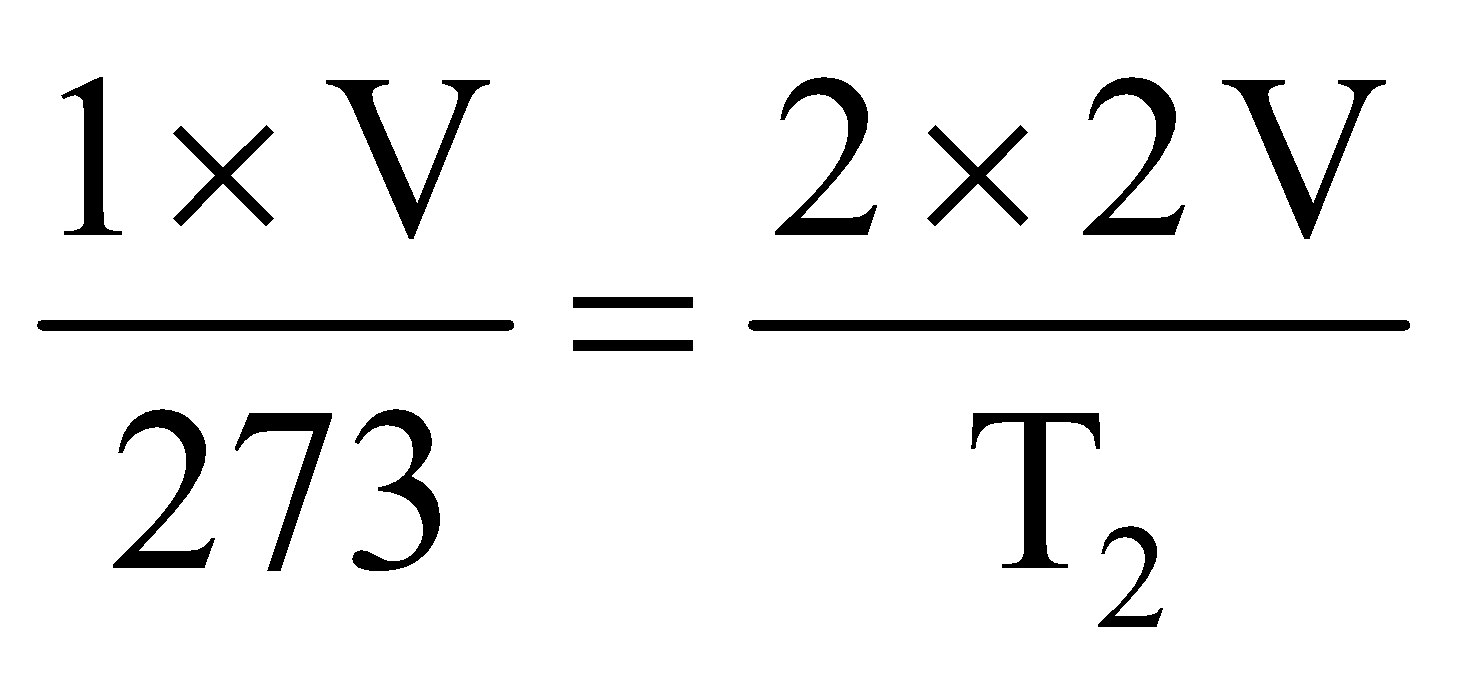
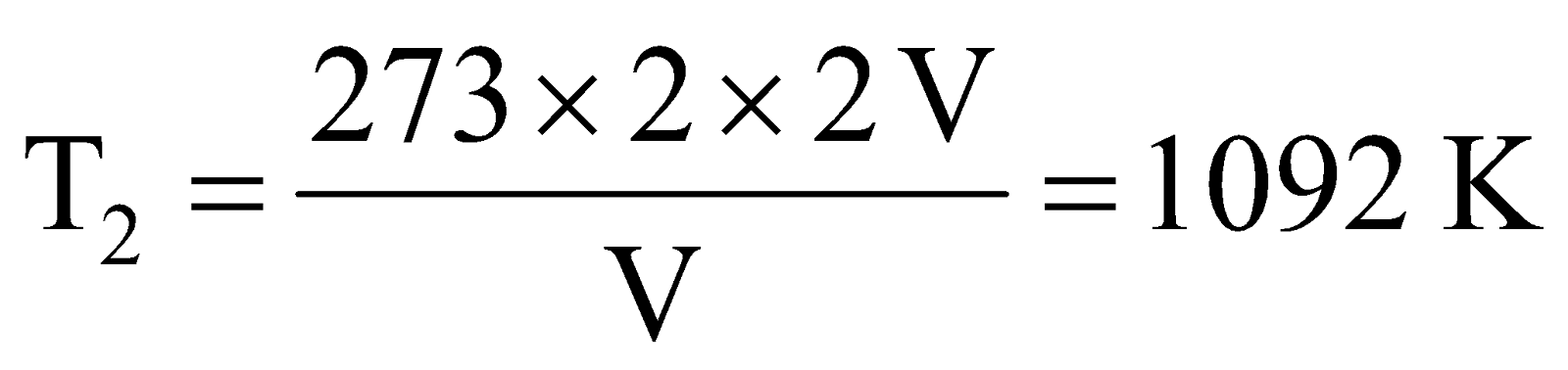
Ideal gas equation:
The equation, which gives the relationship between the four measurable variables viz. P, V, T and n of a gas is called ideal gas equation. It can be derived as follows.
According to Boyle’s law. 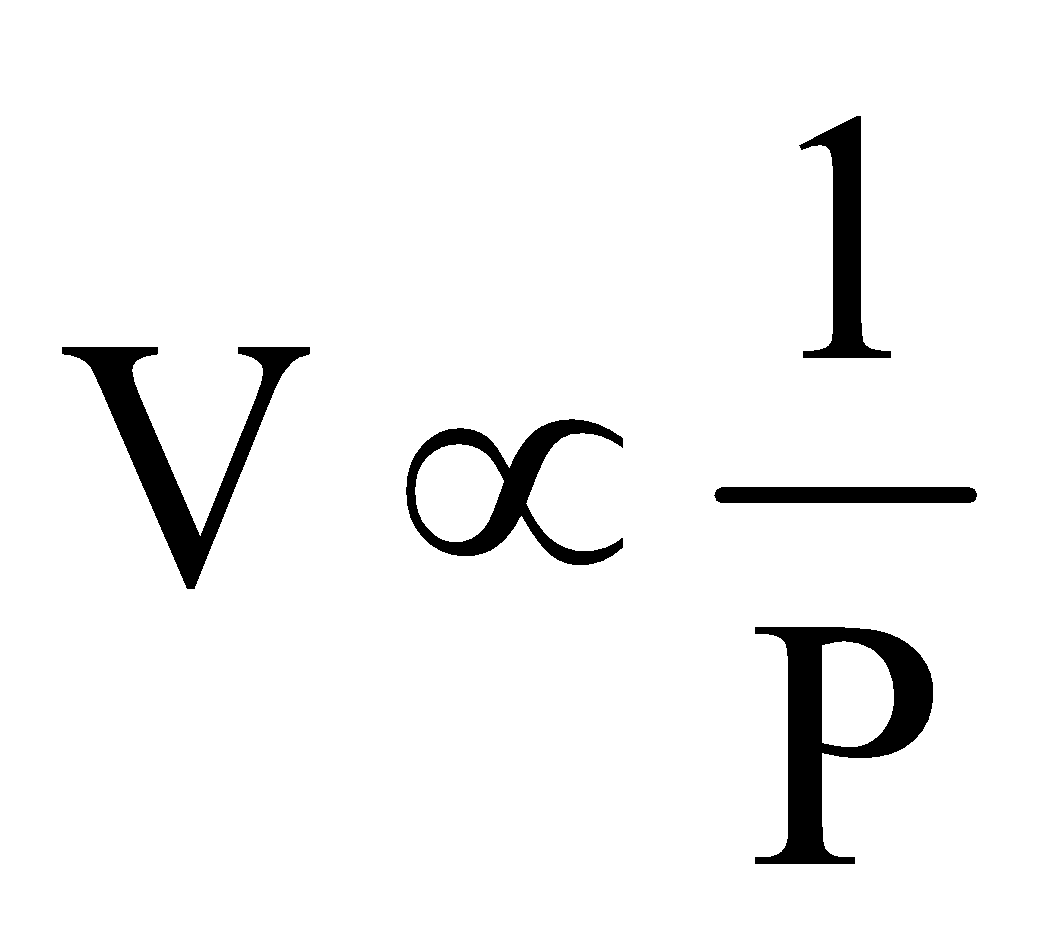 (n, T constant) ... (i)
(n, T constant) ... (i)
According toCharle’s law. 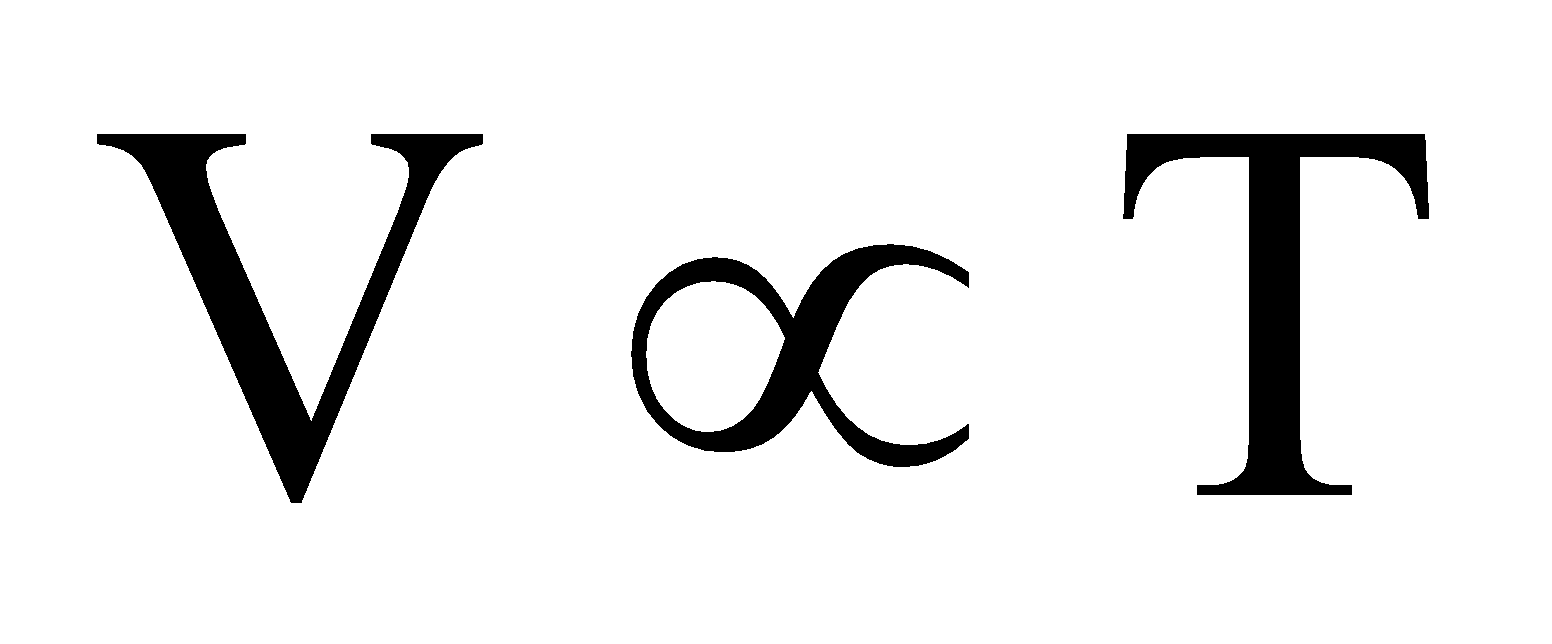 (n, P constant) ... (ii)
(n, P constant) ... (ii)
According to Avogadro’s law. 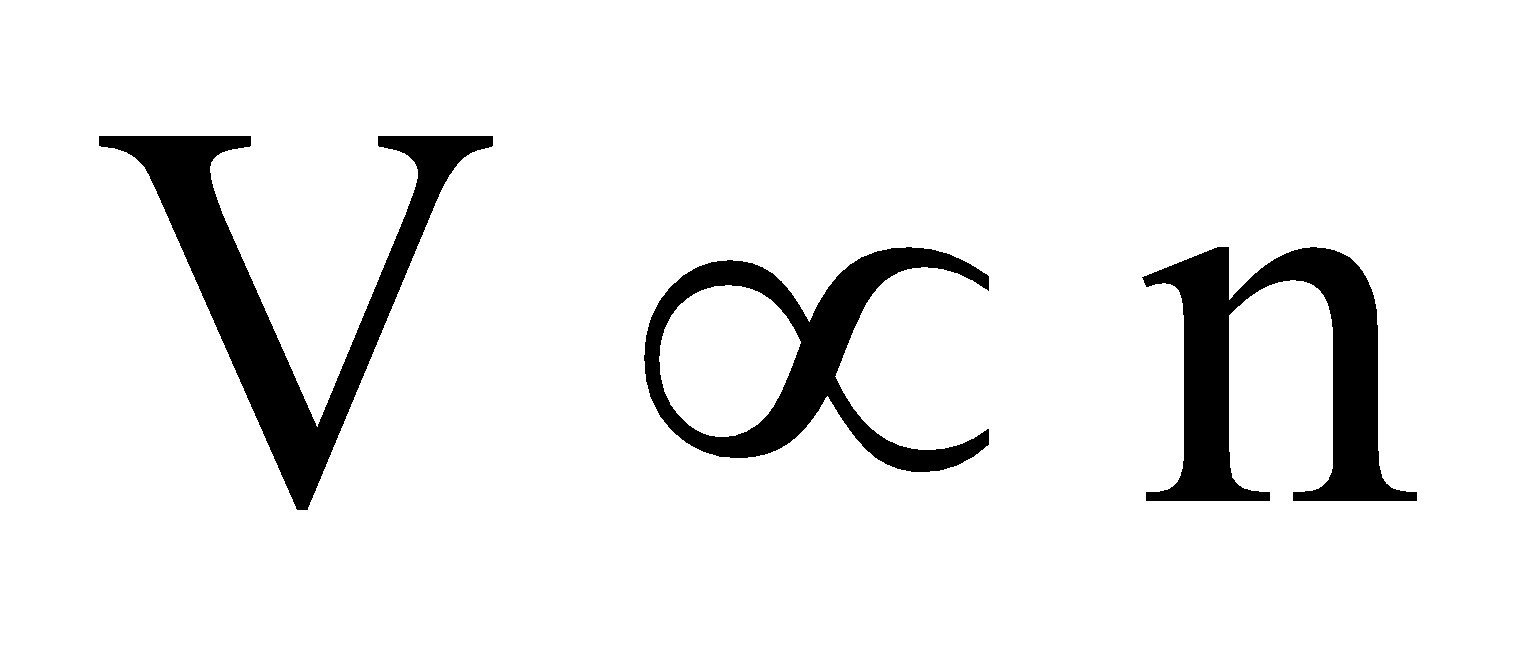 (T, P constant) ... (iii)
(T, P constant) ... (iii)
Combining equations (i), (ii) and (iii), we get,
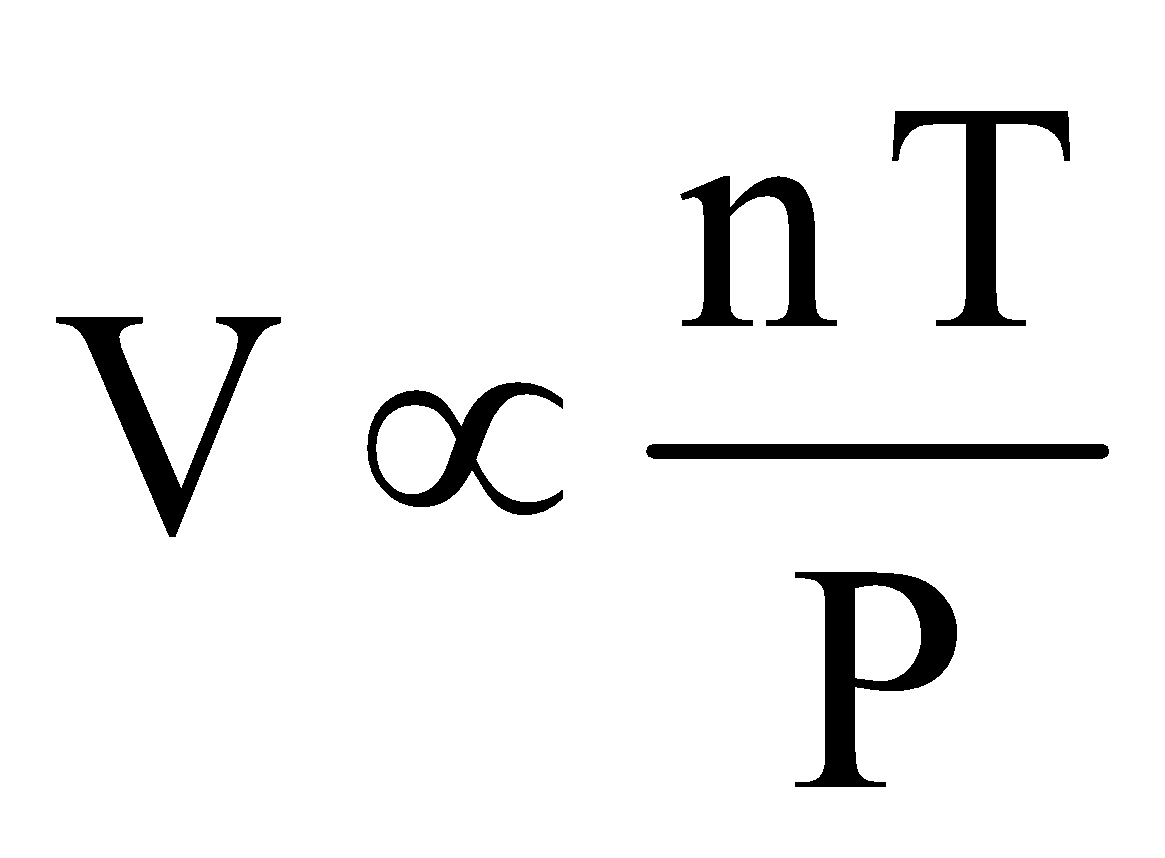 , or
, or 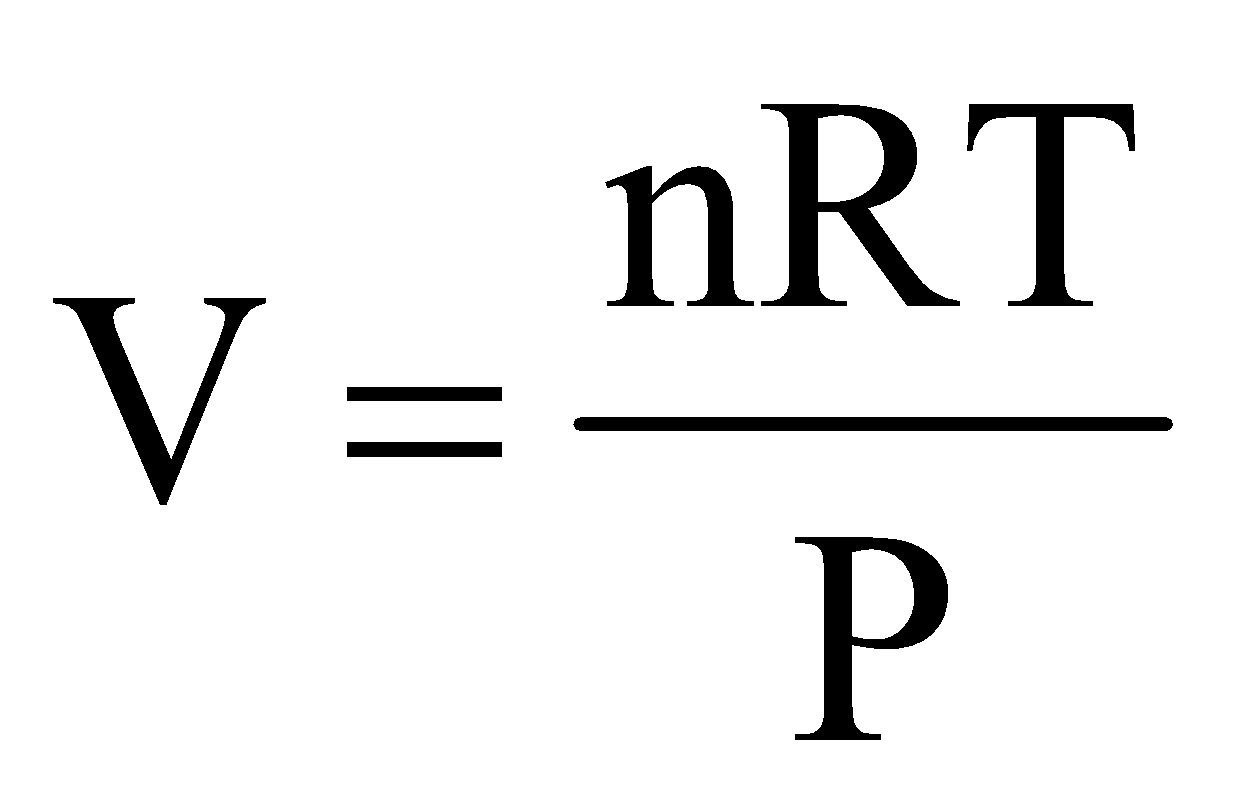
where, R is called universal gas constant.
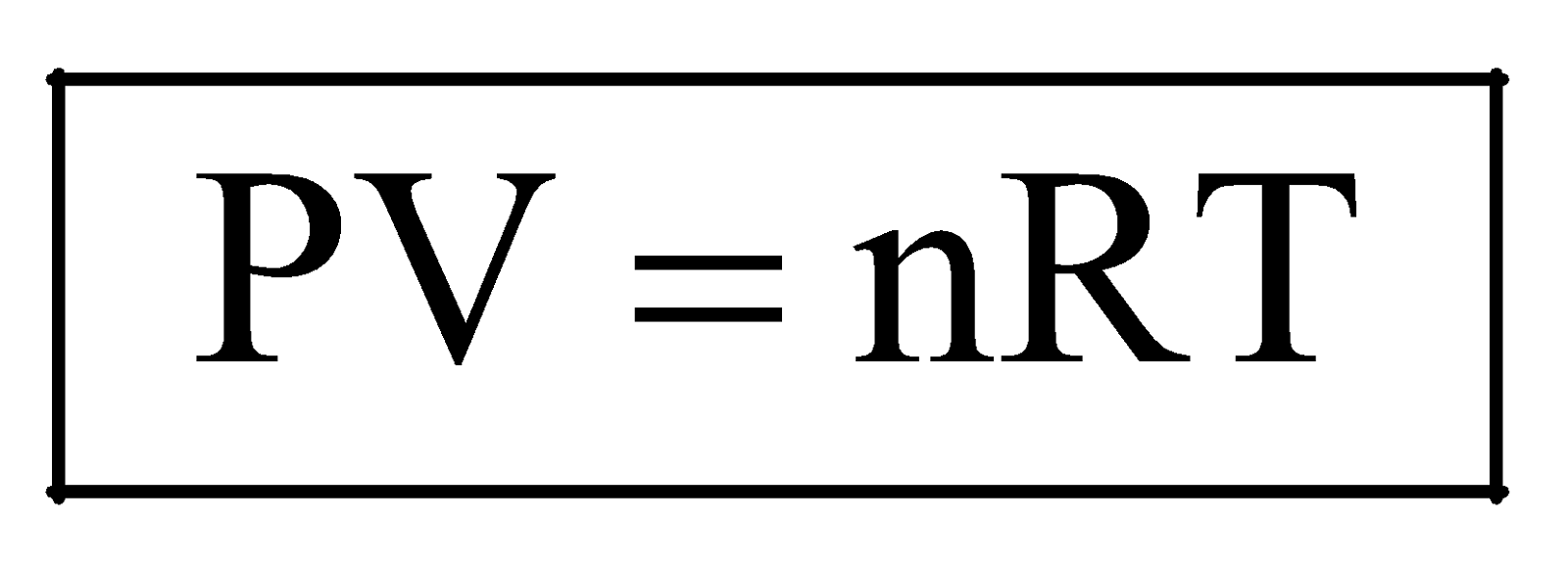 ... (iv)
... (iv)
Equation (iv) is known as ideal gas equation.
Calculation of universal gas constant ‘R’.
From ideal gas equation, 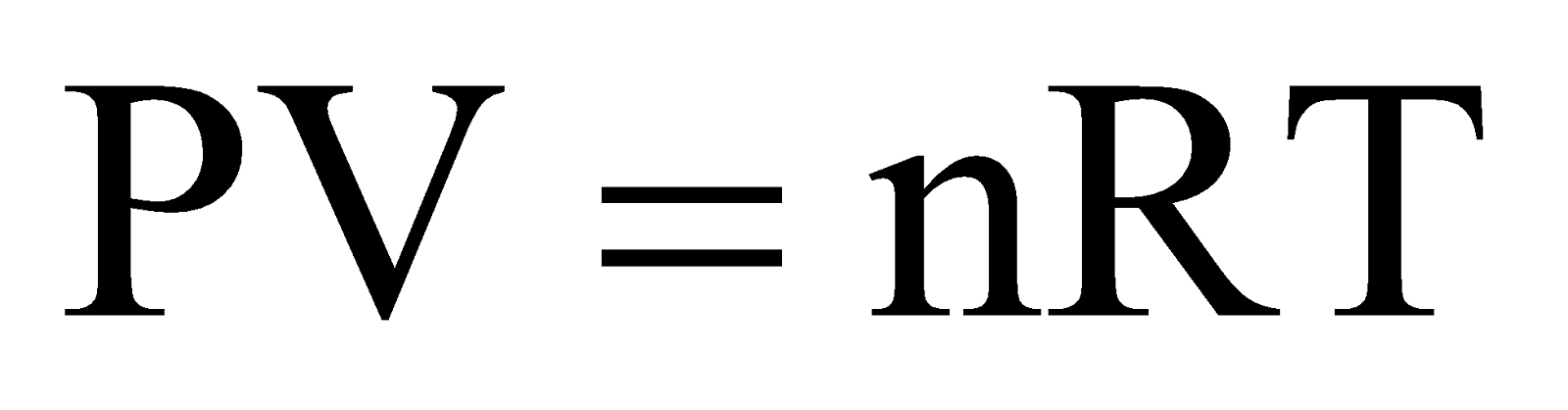 , we have,
, we have,
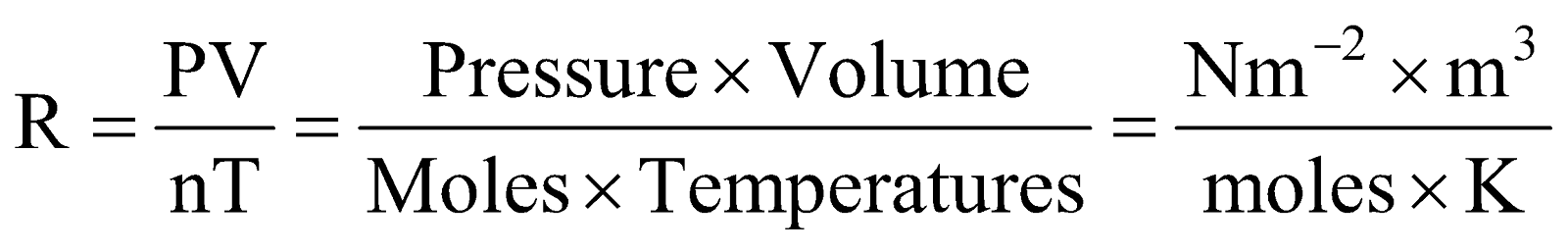 .
.
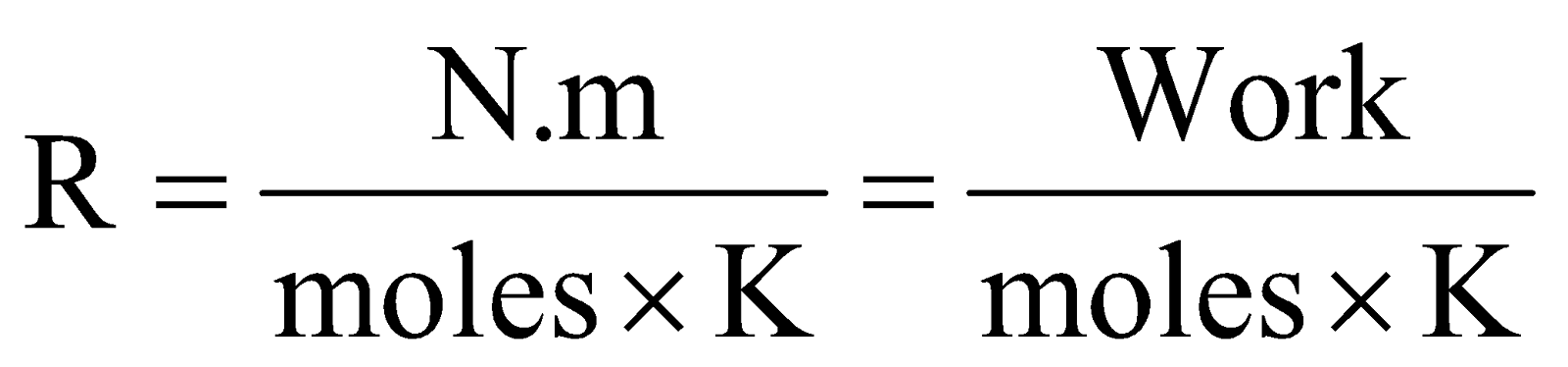 .
.
Thus, R is work done per degree per mole, i.e., gas constant ‘R’ represents the amount of work (or energy) that can be obtained from one mole of a gas when its temperature is raised by one degree.
Numerical values of R. We know that, 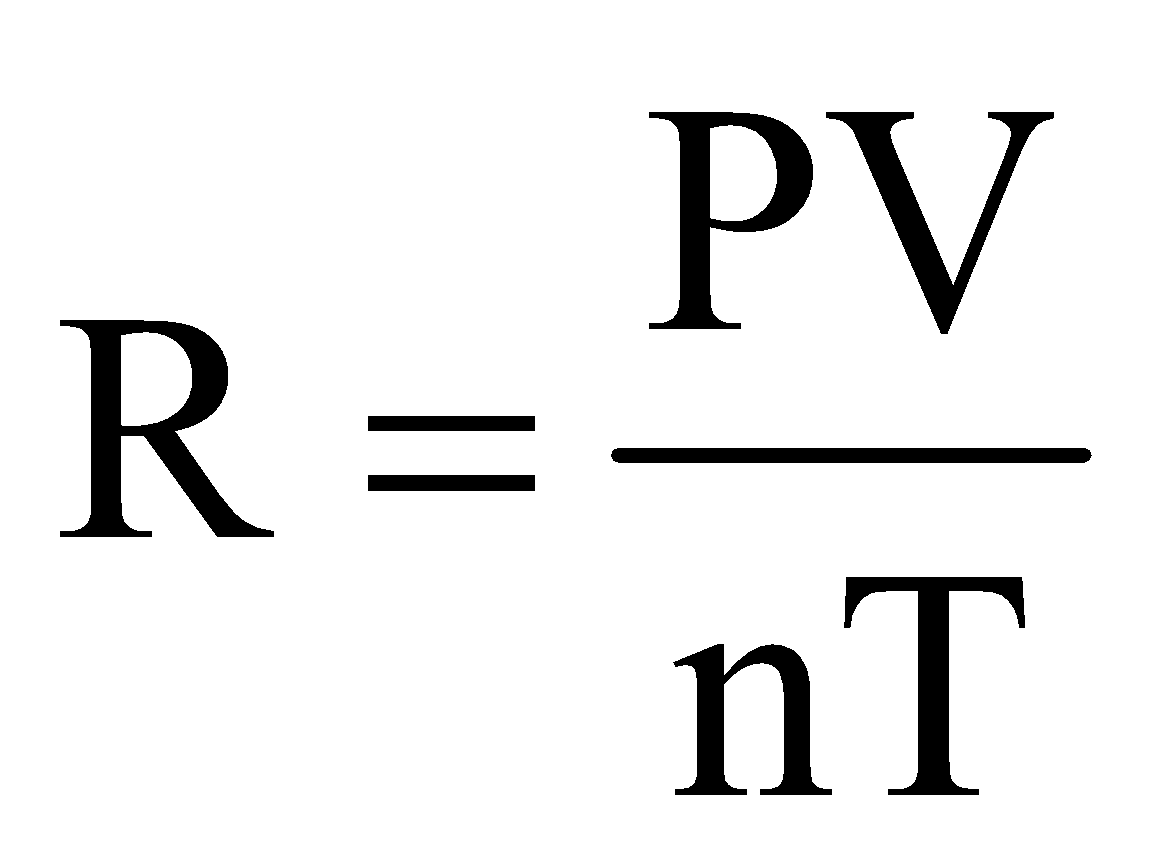 , therefore, magnitude of values of R depends upon the units in which pressure, volume and temperature are expressed, e.g.,
, therefore, magnitude of values of R depends upon the units in which pressure, volume and temperature are expressed, e.g.,
(i) In S.I. units for one mole of gas at S.T.P.
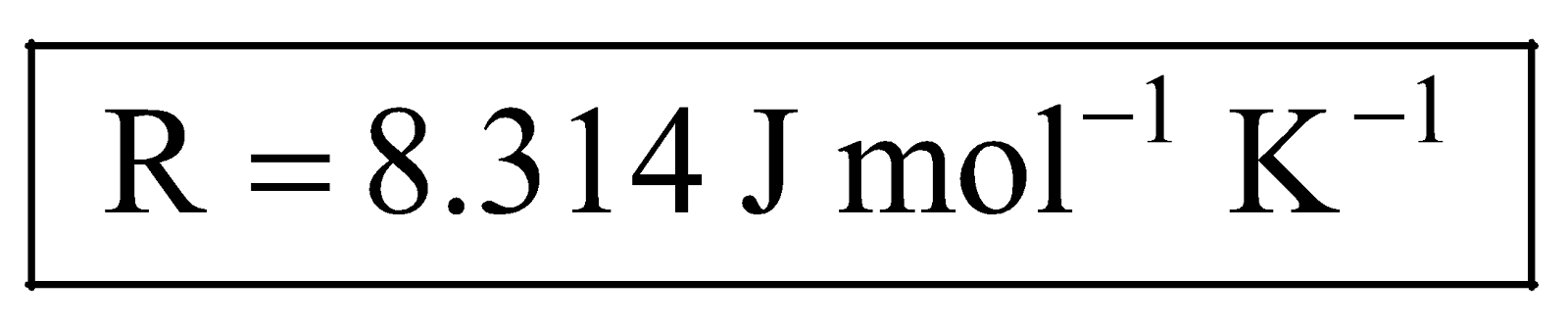
 .
.
(ii) In conventional units, for one mole of gas at S.T.P. and A.S.T.P.
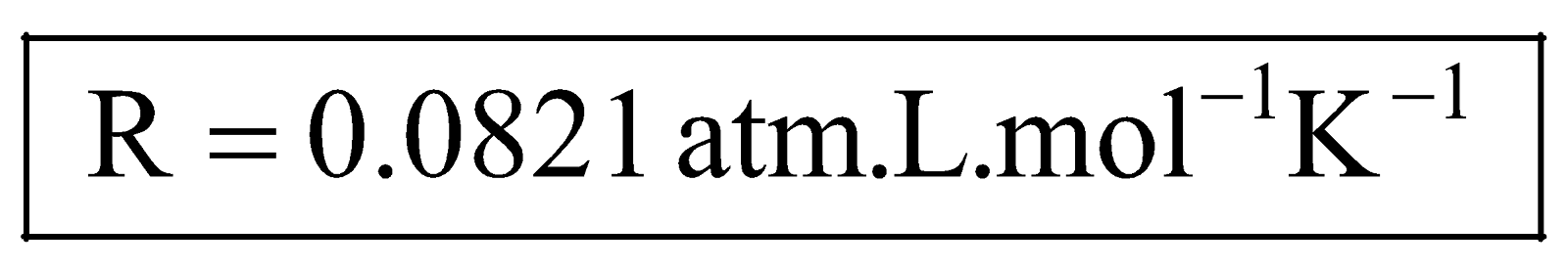 .
.
Under A.S.T.P. conditions for one mole of a gas, we have
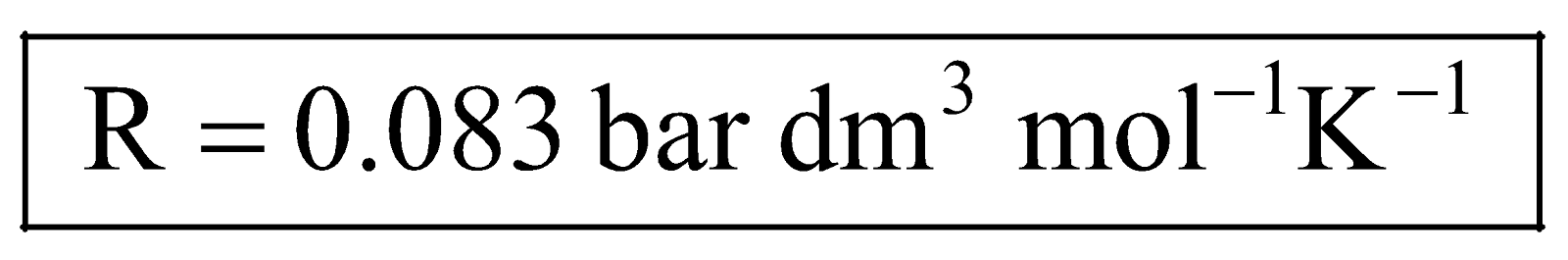 .
.
Example 5 Helium gas collected over water measures 350 ml at 20°C. If atmospheric pressure is 752.5 mm of Hg and vapour pressure of water at 20°C is 17.5 mm of Hg, what weight of helium has been collected and what is the percentage weight of water vapour in the moist helium gas?
Solution
PV = 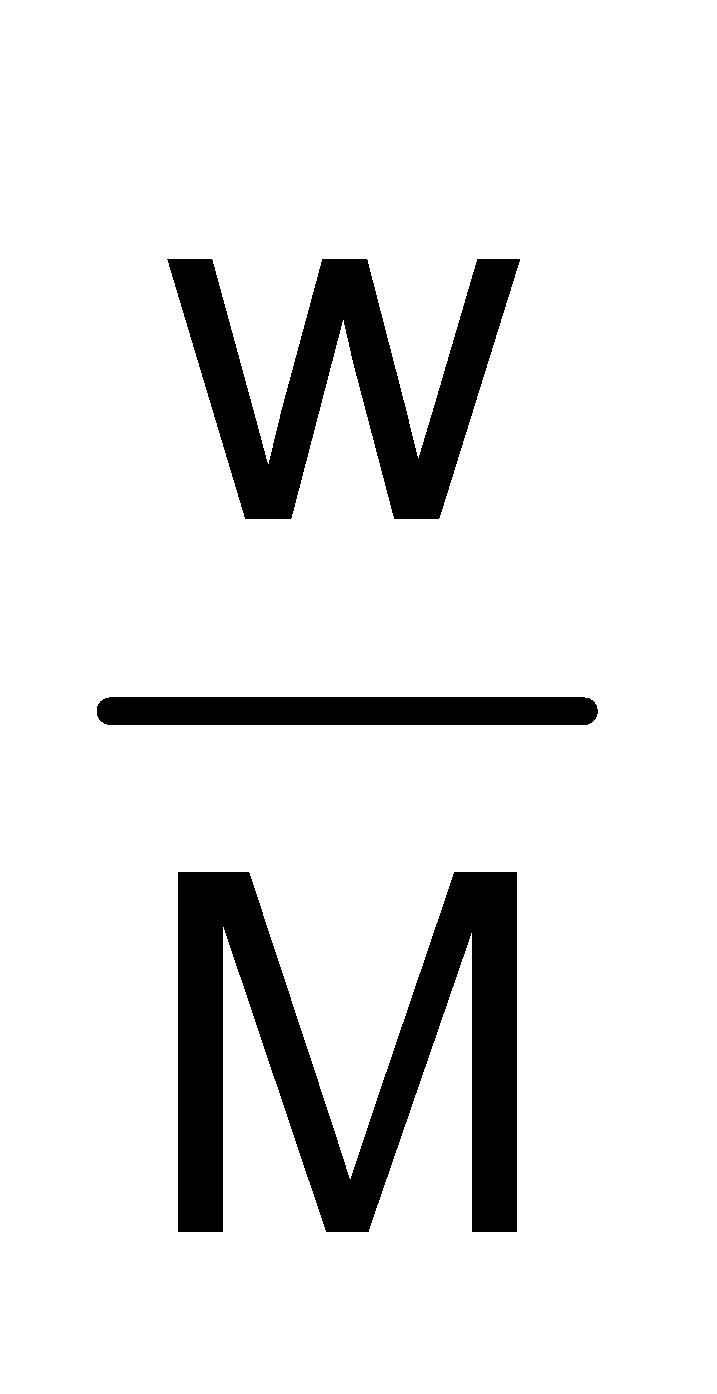 RT ∴ w =
RT ∴ w = 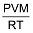 …(i)
…(i)
we know that
P = PHe + PVap
Here, P = atmospheric pressure
PHe = pressure of dry helium gas
PVap = vapour pressure of water
∴ PHe = (752.5 - 17.5) mm = 735 mm = 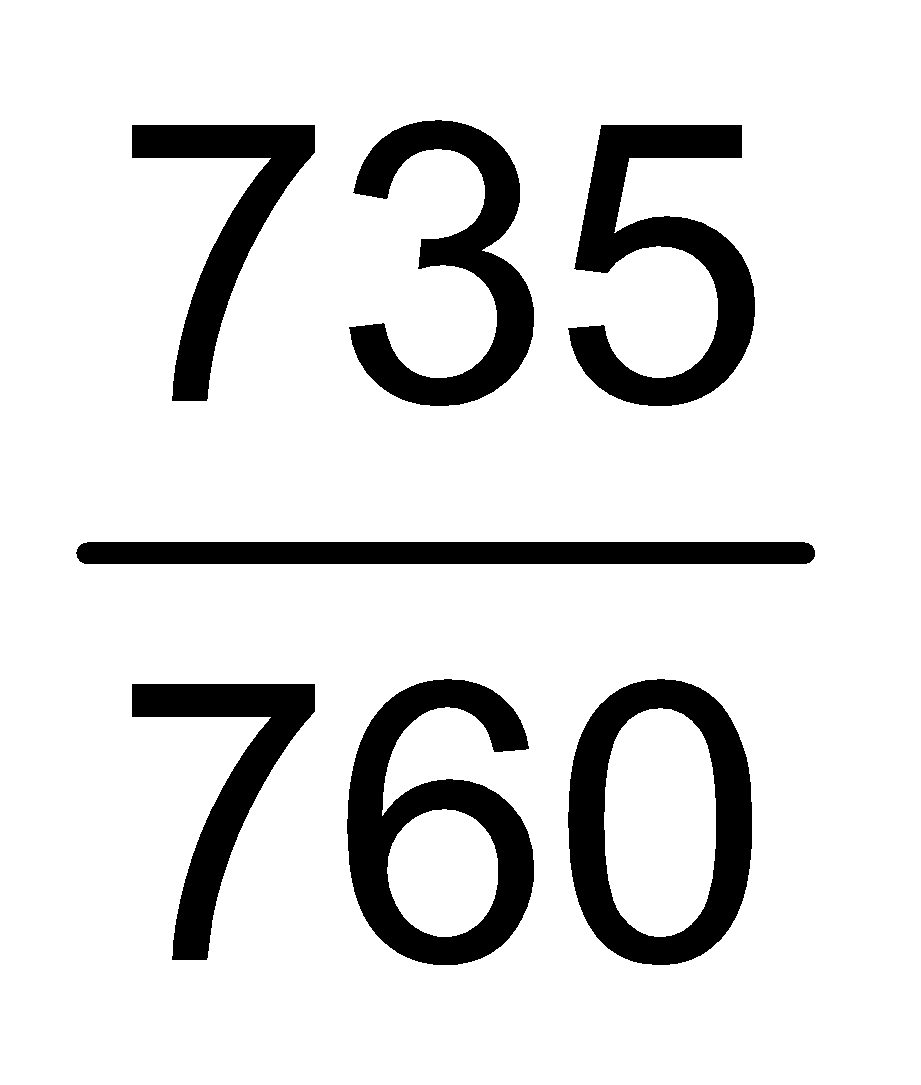 atm.
atm.
∴ wHe = 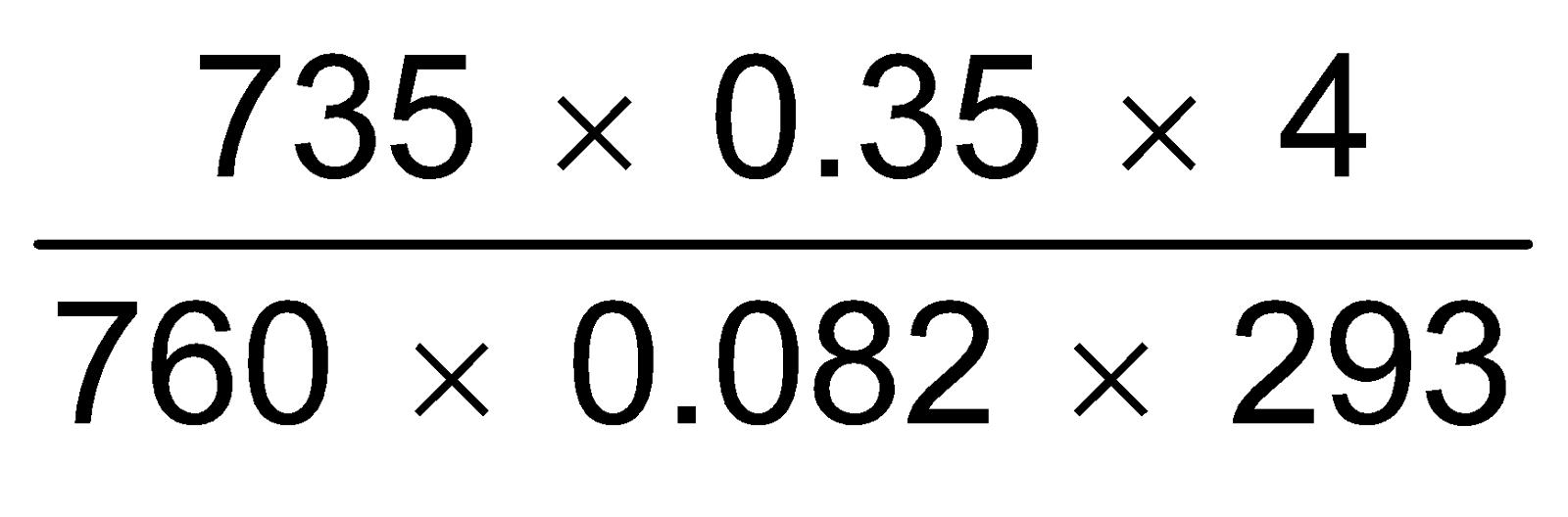 = 0.0564 gm
= 0.0564 gm
∴ wt. of helium = 0.0564 gm
∴ 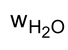 =
= 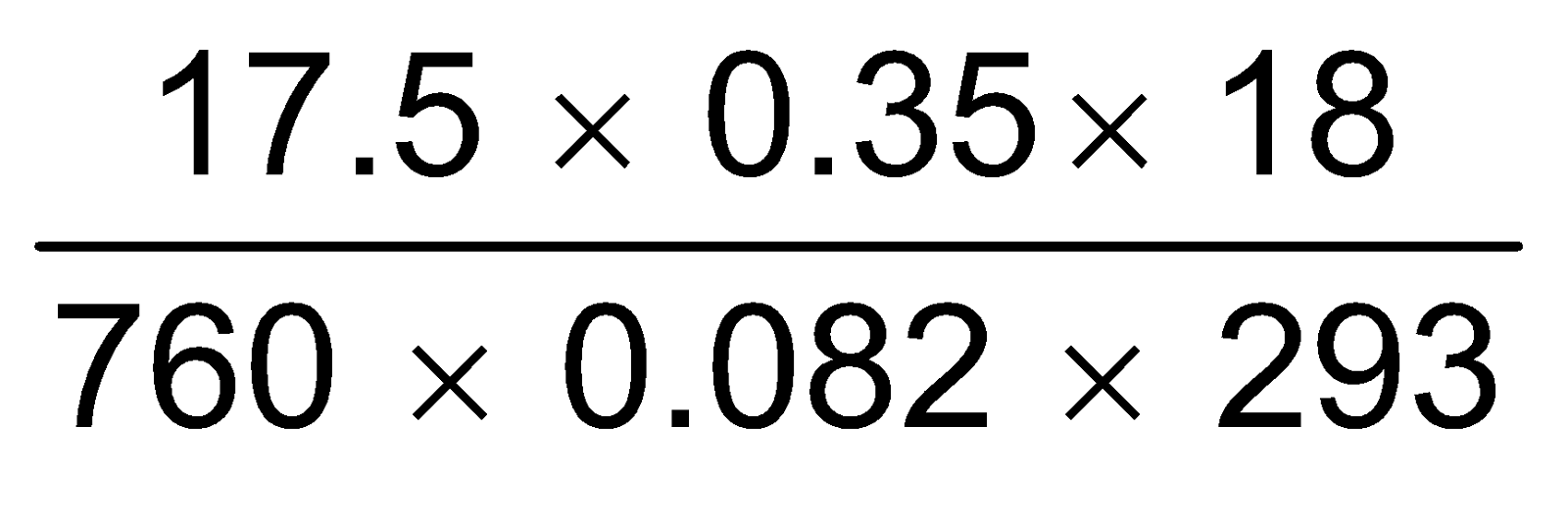 = 0.00604 gm = 6.04 mg.
= 0.00604 gm = 6.04 mg.
∴ Percentage weight of water vapour in moist helium gas
= 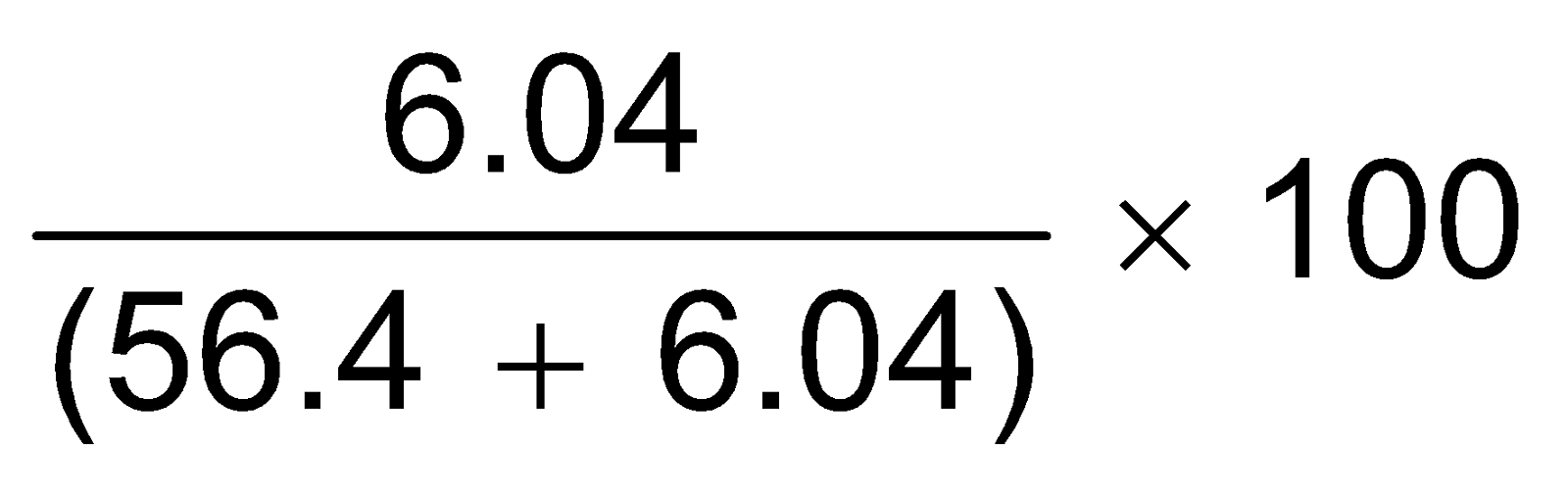
= 9.67%










