DALTON’S LAW OF PARTIAL PRESSURE

DALTON’S LAW OF PARTIAL PRESSURE

According to this law total pressure of a non reacting mixture of gases is equal to the sum of partial pressures of individual gases.

P = PA + PB + PC + ……………….. (in mixture of gases which do not react chemically)

Let nA moles of A, nB moles of B and nC moles of C are filled in a vessel of volume V maintained at temperature T. Then, total pressure will be

PV = (nA + nB + nC)RT (Gas equation) …..(i)

Let only nA moles of A is added in the vessel then

PAV = nART …..(ii)

Similarly,

PBV = nBRT …..(iii)

PCV = nCRT …..(iv)

On adding, (ii), (iii) and (iv) we get

(P_A + P_B + PC)_V = (n_A + n_B + n_C) RT …..(v)

Now comparing equation (i) and (v) we get

Alternatively

Dividing equation (ii) by (i)

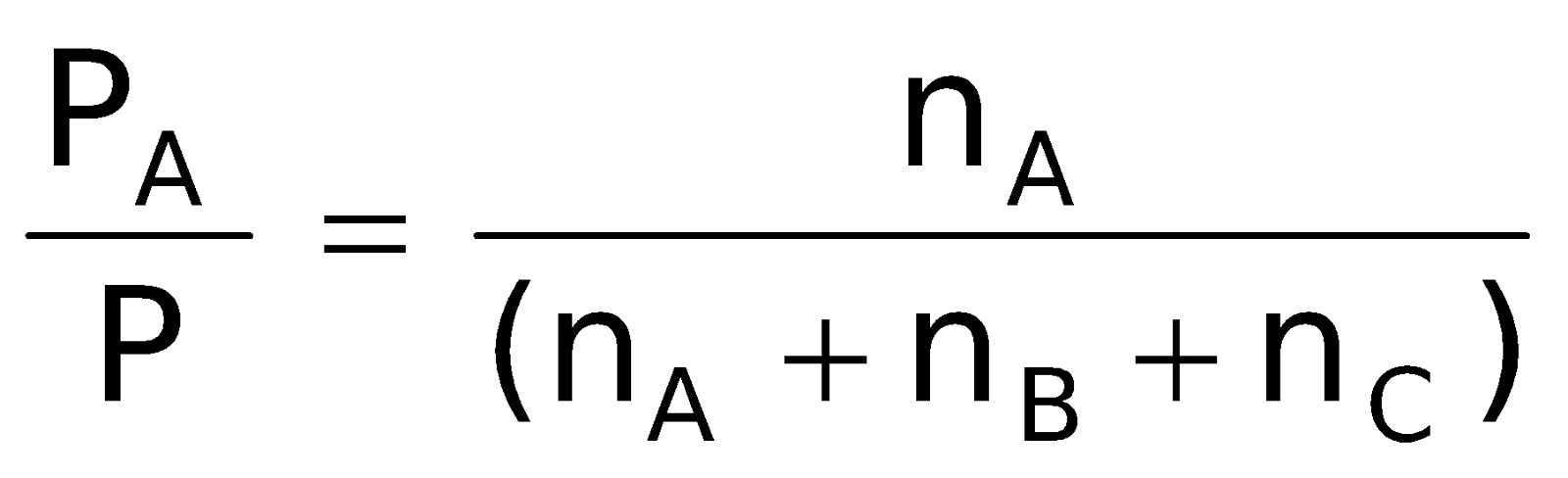= XA (mole fraction of A)

PA = PXA …..(i)

Since, PB = PXB …..(ii)

PC = PXC …..(iv)

on adding (i), (ii) and (iii) we get

(P_A + P_B + P_C) = P (X_A + X_B + X_C)

Similarly, XA  + XB + XC =1

So,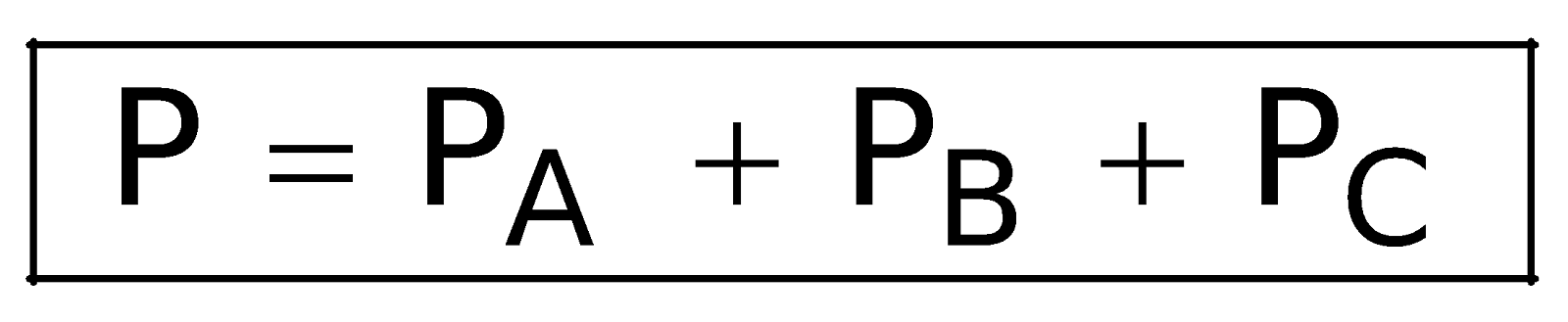

The law can even be applicable to a mixture of reacting gases under the condition when they have attain equilibrium (at which the number of moles of each constituent species remains fixed.

Example6   A 2.5 litre flask contains 0.25 mole each of sulphur dioxide and nitrogen gas at 27°C. Calculate the partial pressure exerted by each gas and also the total pressure.

Solution: Partial pressure of SO2

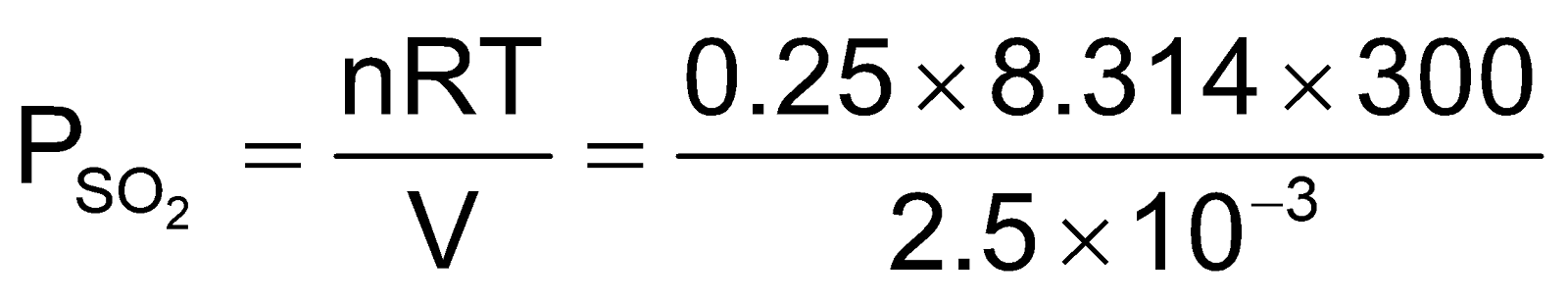
= 2.49 × 105 Nm–2 = 2.49 × 105 Pa

Similarly 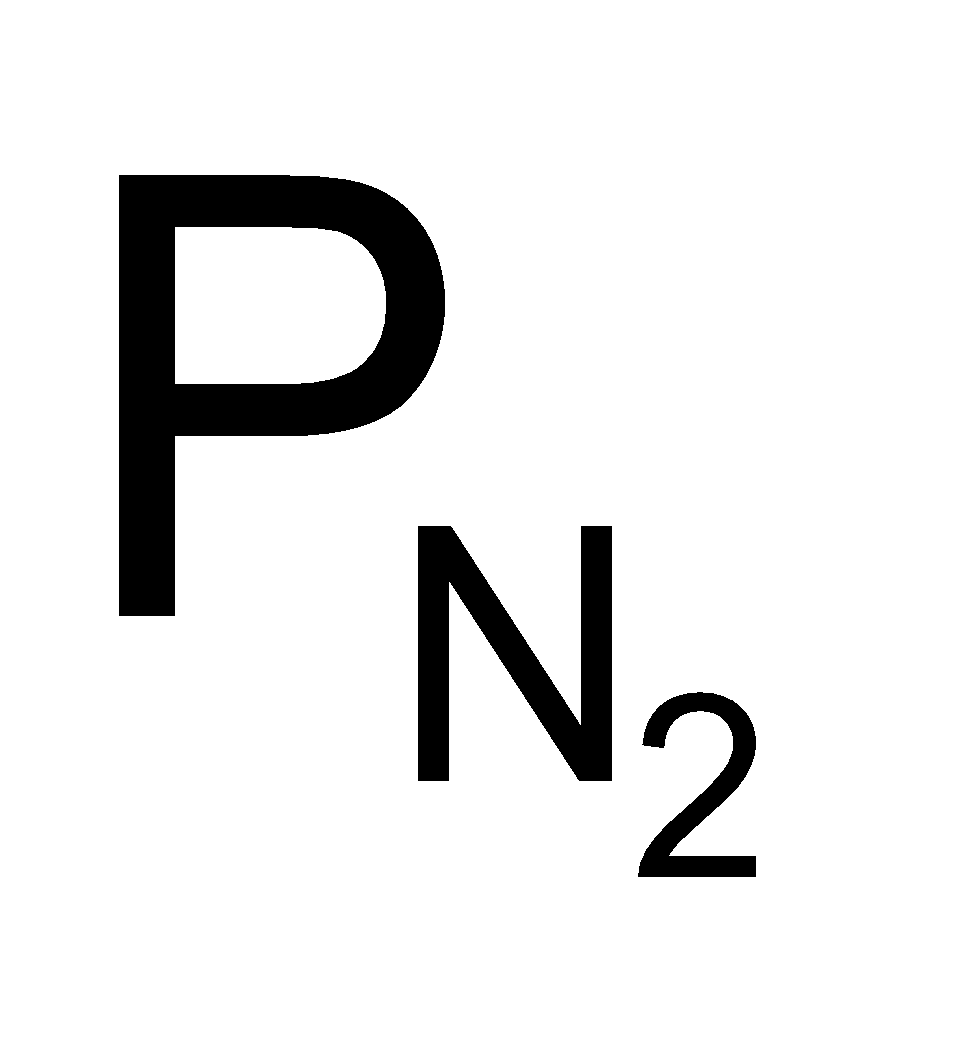= 2.49 × 105 Pa

Following Dalton’s Law

P Total = +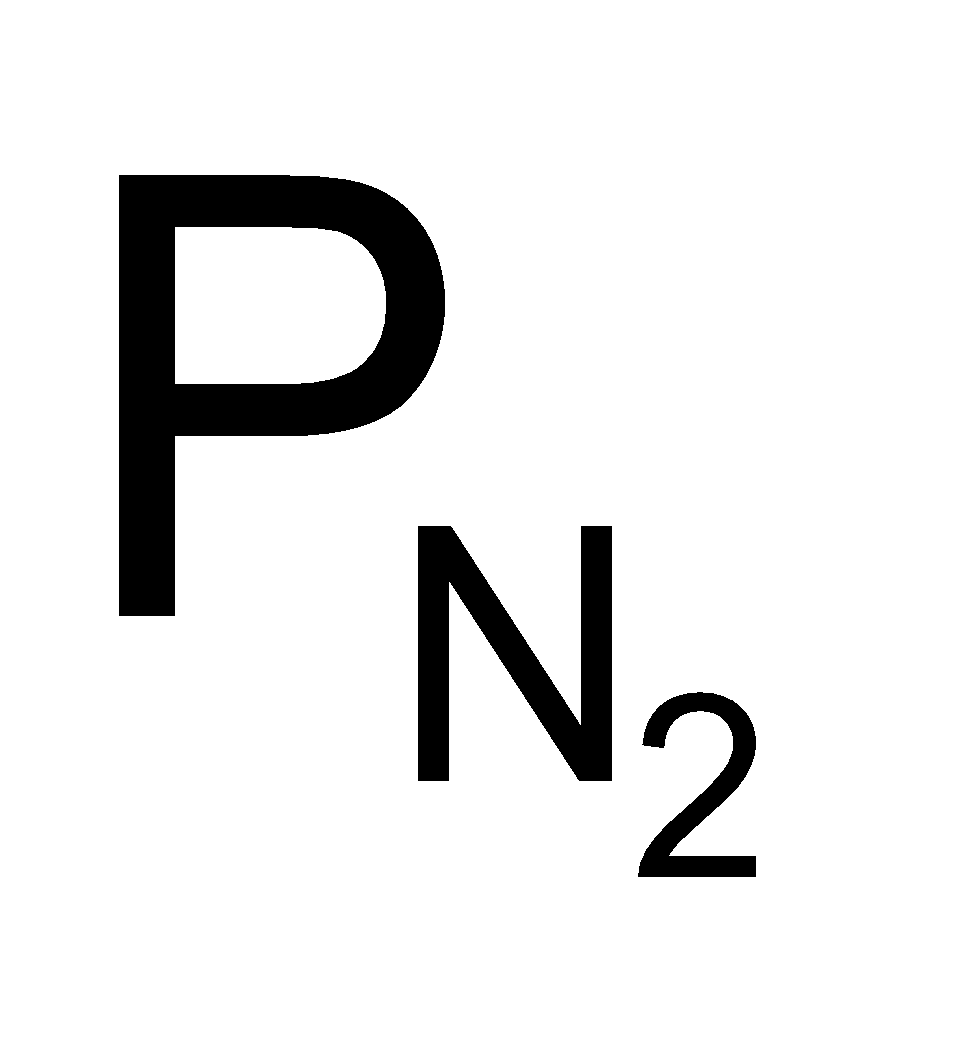

= 2.49 × 105 Pa + 2.49 × 105 Pa = 4.98 × 105 Pa