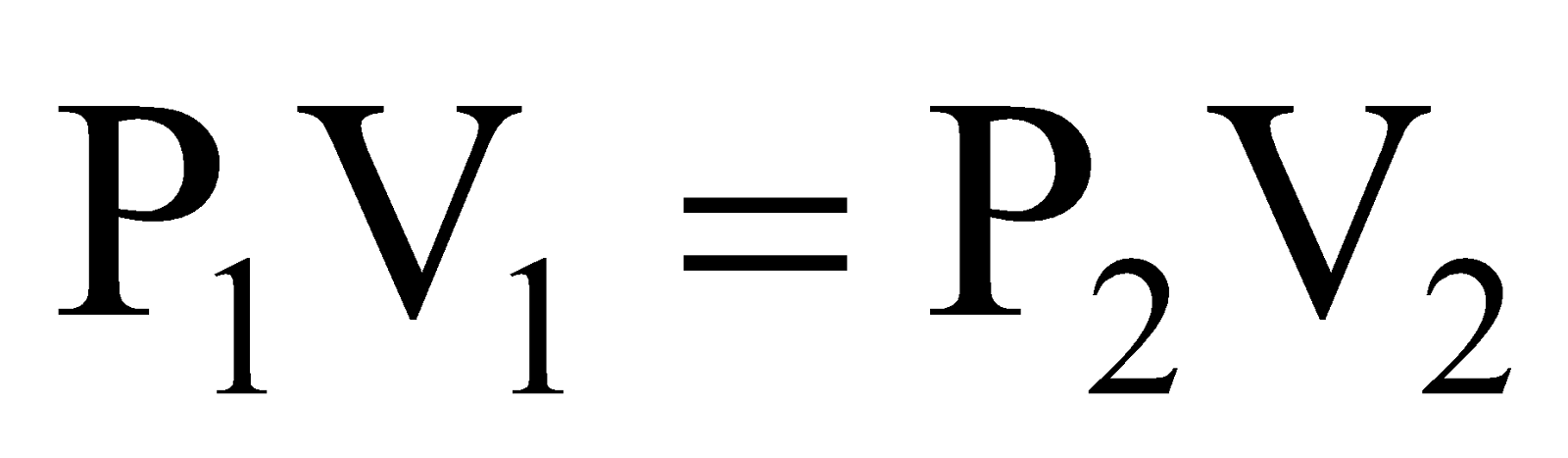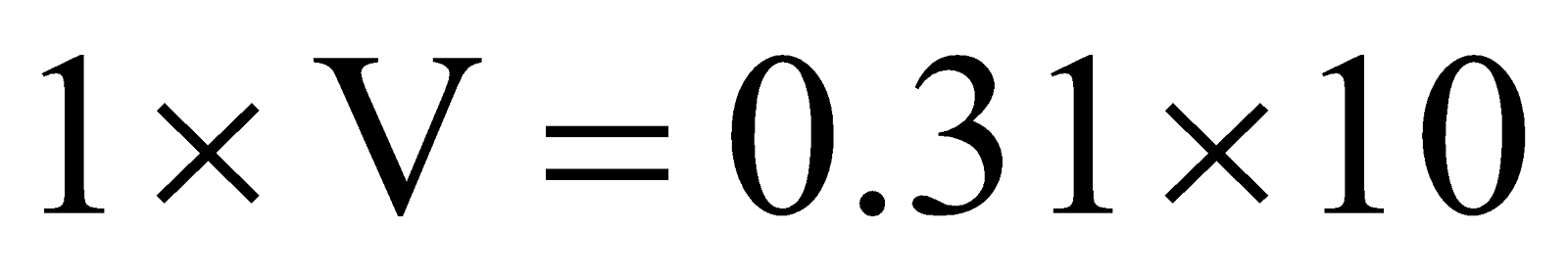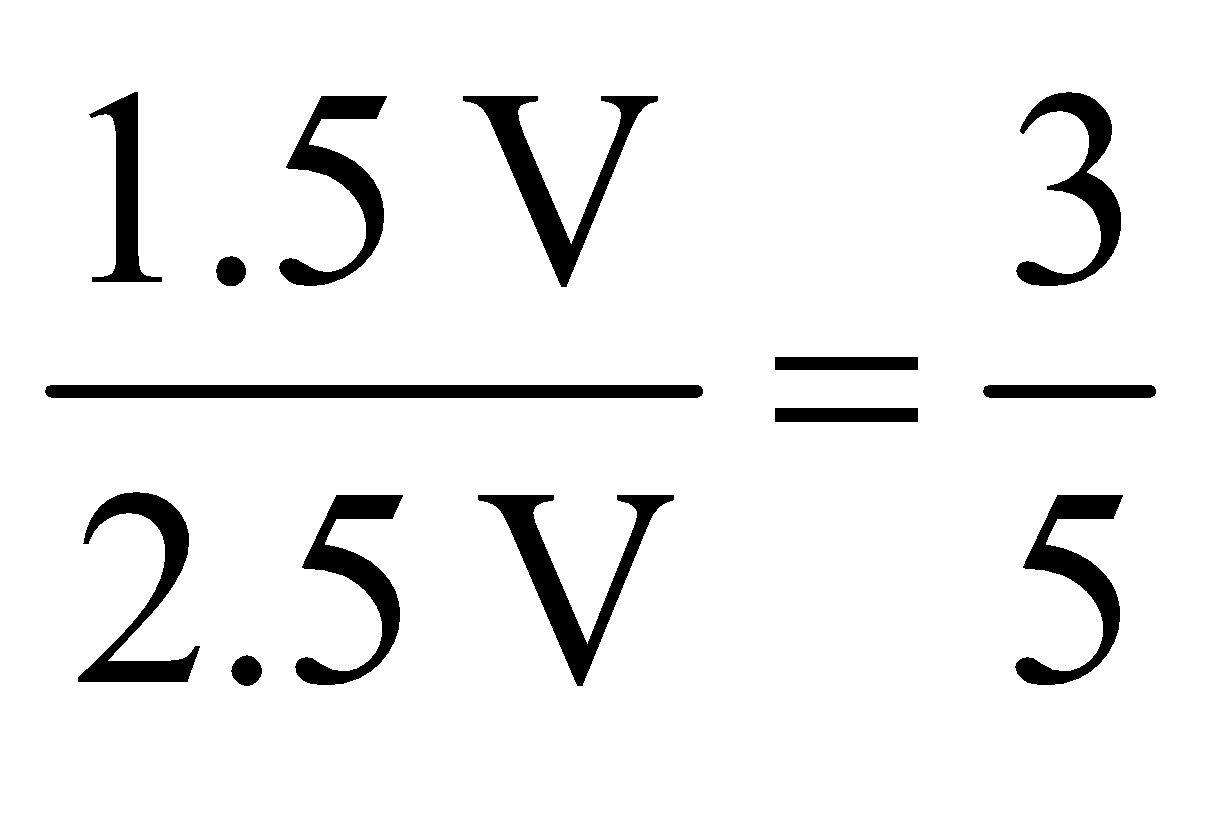Introduction
States of matter of Class 9
A substance is regarded as a gas if its boiling point is below the room temperature under atmospheric pressure. For example, the boiling points of H2, CO2, O2, etc. are below room temperature, therefore, these are regarded as gases. In general gases have following physical properties.
- Gases do not have definite shape and volume. They acquire the shape and volume of container in which they are placed. Volume of gases will change with changing temperature and pressure.
- Gases exert uniform pressure on the walls of container in all directions.
- Gases diffuse rapidly through each other to form a homogenous mixture.
- Gases are highly compressible and their volume decreases by increasing the pressure and vice versa.
In addition to the properties of gases listed above, gases also obey certain laws called “Gas laws”. Gas laws give quantitative relationships between some measurable parameters like. mass, volume, temperature and pressure of the gas. These parameters are discussed below.
MEASURABLE PROPERTIES OF GASES
Mole, volume, temperature are the important measurable properties of gases.
- Mole: The mole of the gas can be calculated by
n = 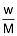
Where n = number of moles
w = mass of gas in grams
M = molecular mass of the gas
Volume: Since gases occupy the entire space available to them, therefore the gas volume means the volume of the container in which the gas is enclosed.
Units of Volume:Volume is generally expressed in litre or cm3 or dm31m3 = 103 litre = 103 dm3 = 106 cm3.
Pressure: The force exerted by the gas per unit area on the walls of the container is equal to its pressure.
Units of Pressure: The pressure of a gas is expressed in atm, Pa, Nm–2, bar or, lb/In2 (psi).
760 mm = 1 atm = 10132.5 KPa = 101325 Pa = 101325 Nm–2
760 mm of Hg = 1.01325 bar = 1013.25 milli bar = 14.7 lb/2n2 (psi)
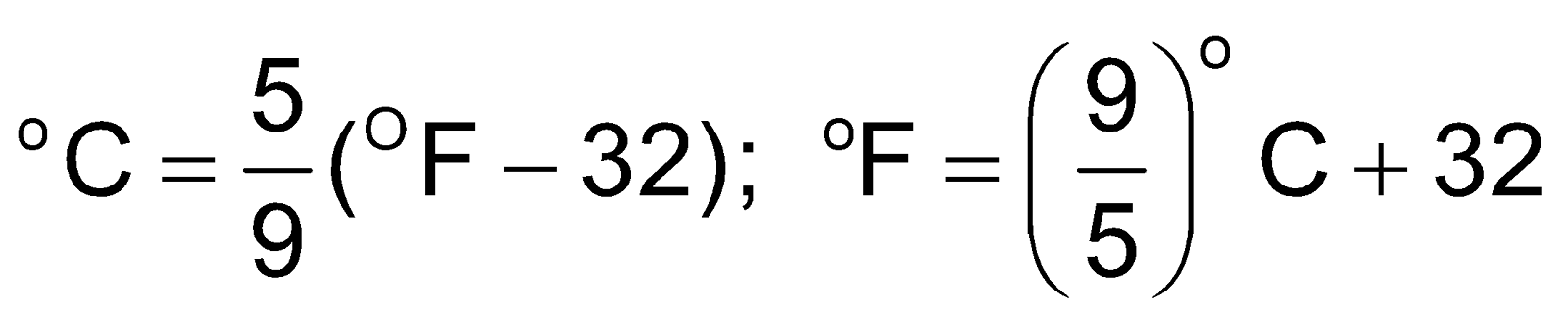
Temperature: Temperature is defined as the degree of hotness. The SI unit of temperature is Kelvin. On the Celsius scale water freezes at 0°C and boils at 100°C where as in the Kelvin scale water freezes at 273 K and boils at 373 K.
Note :Some conversion:
1 m3 = 10 dm3 = 106 cm3
1 ml = 1 cm3, 1 litre =103 cm3=1 dm3=10–3 m3
1 atm = 760 mm of Hg, 76 cm of Hg
1 atm = 760 torr
1 atm = 1.01325 bar, 1 bar = 0.987 atm
1 atm = 1.01325 × 105 Pascal,
1 bar = 105 Pascal
1 atm = 1.01325 × 102KPa, 1 bar = 102KPa
1 Pa = 1 Nm–2 (Pa is the SI unit)
= 1 kg m–1 s–2
–273.15oC = 0 K = absolute zero temperature
toC = t + 273.15 K
GAS LAWS
The state of a sample of gas is defined by 4 variables i.e. P, V, n & T. Gas laws are the simple relationships between any two of these variables when the other two are kept constant.
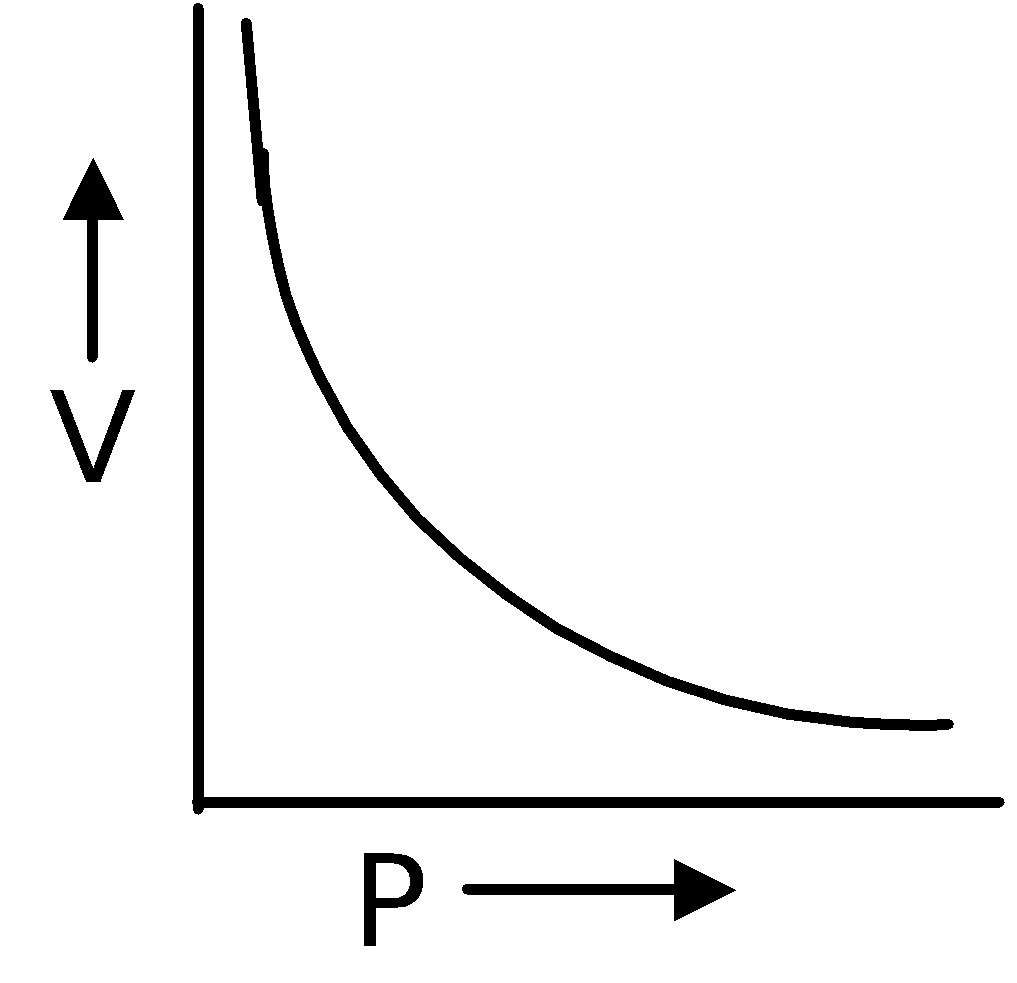
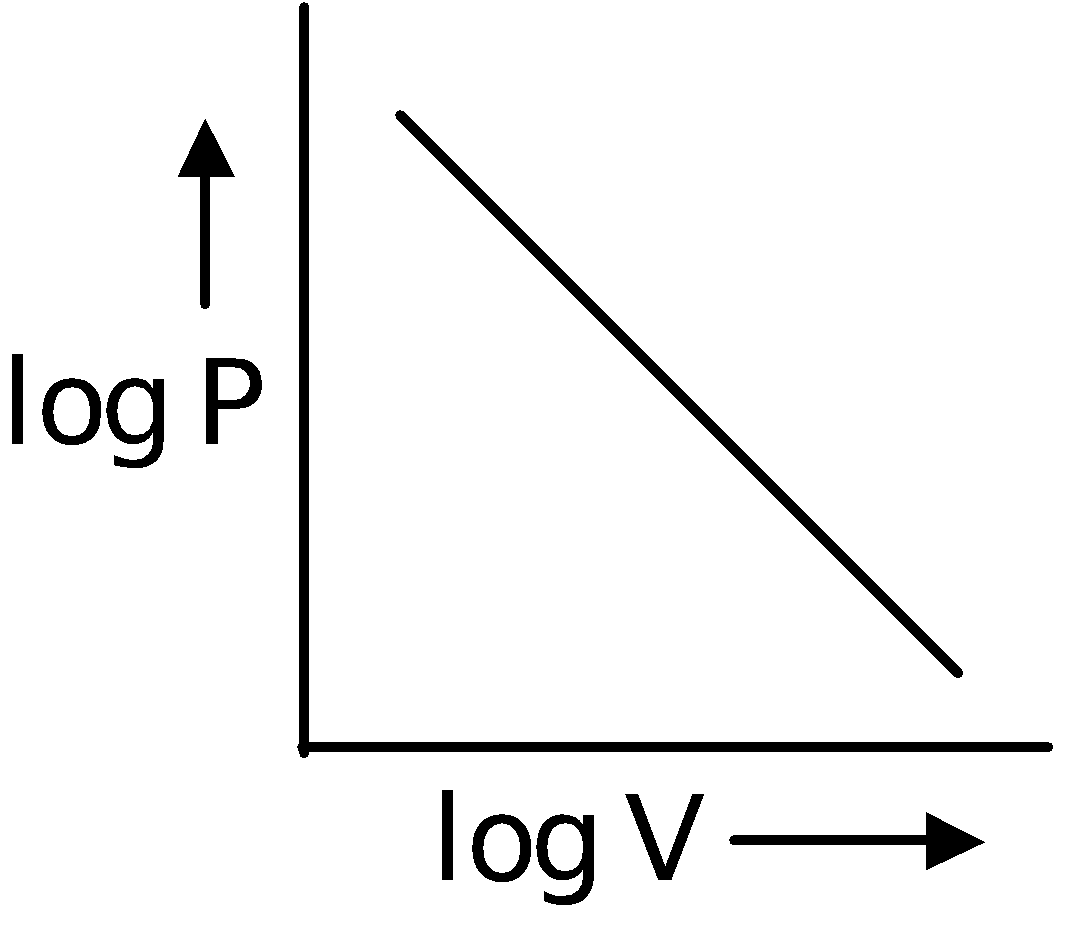
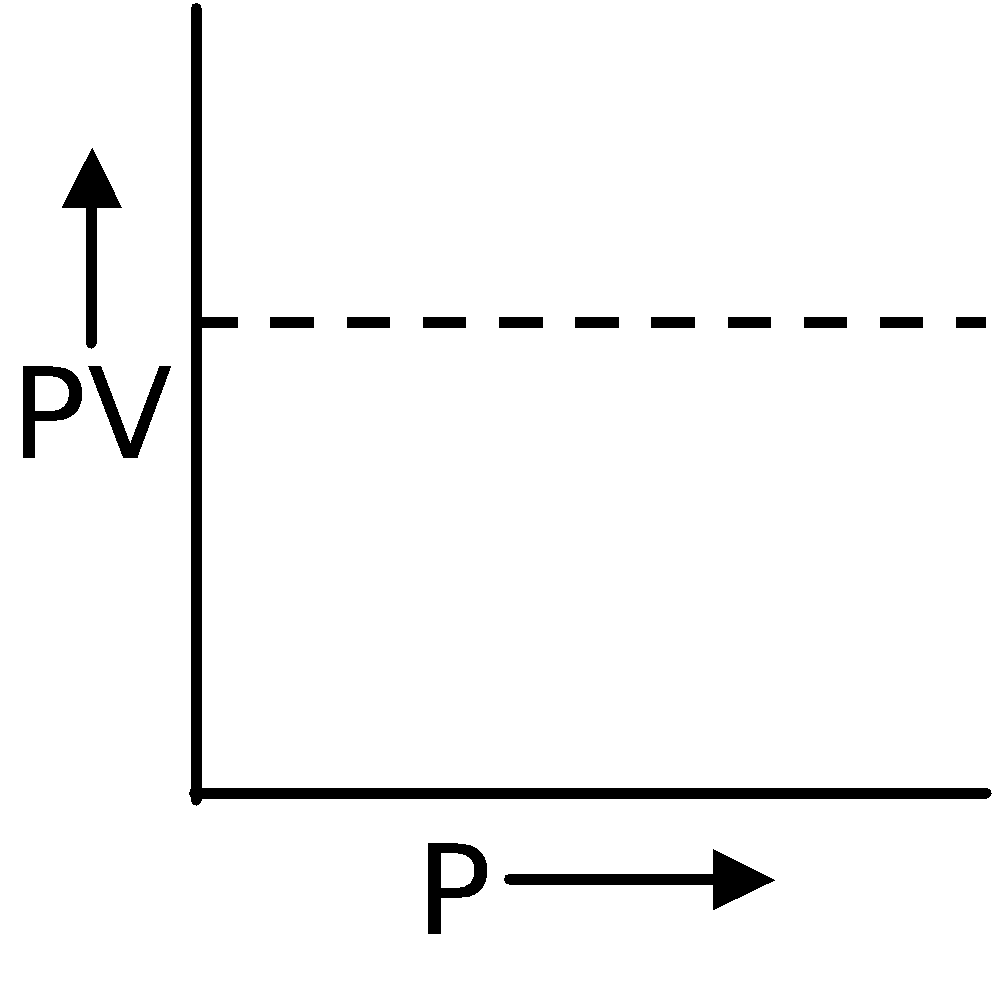
Boyle's Law
In 1662, Robert Boyle discovered that there existed a relation between the pressure and the volume of a fixed mass of gas at a fixed temperature. According to this law, volume of definite mass of gas is inversely proportional to pressure at constant temperature.
∴ V ∝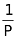 (at constant T and n)
(at constant T and n)
∴ PV = Constant or P1V1 = P2V2
|
(a) |
(b) |
(c) |
Example:1 A 10.0 L cylinder of H2 gas is connected to an evacuated 290.0 L tank. If the final pressure is 700 mm Hg, what must have been the original gas pressure in the cylinder?
Solution. Initial volume, V1 = 10.0 L
Final volume, V2 = 10.0 + 290.0 = 300.0 L
Let initial pressure = P1
Final pressure, P2 = 700 mm Hg (given)
Applying, P1V1 = P2V2, we get
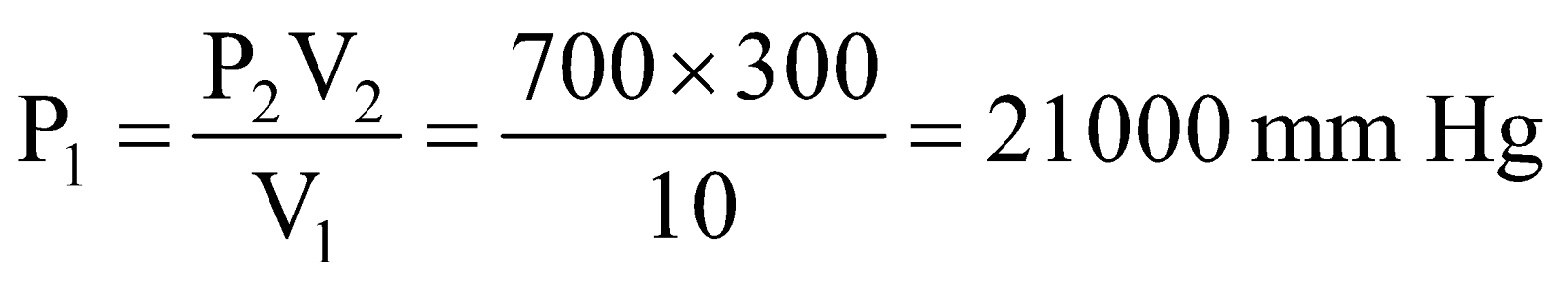
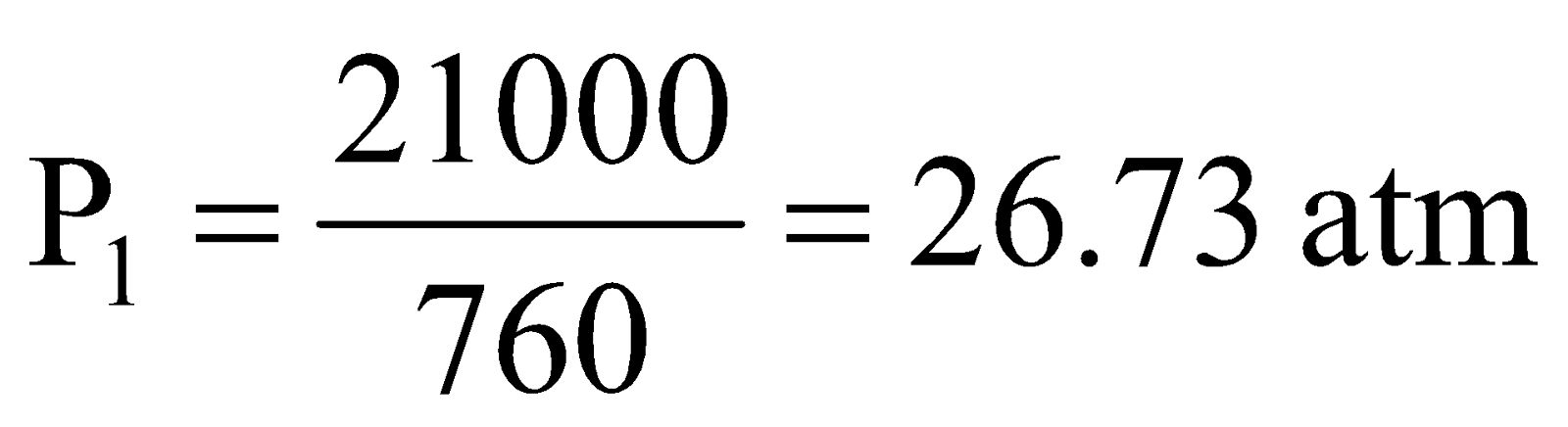 .
.

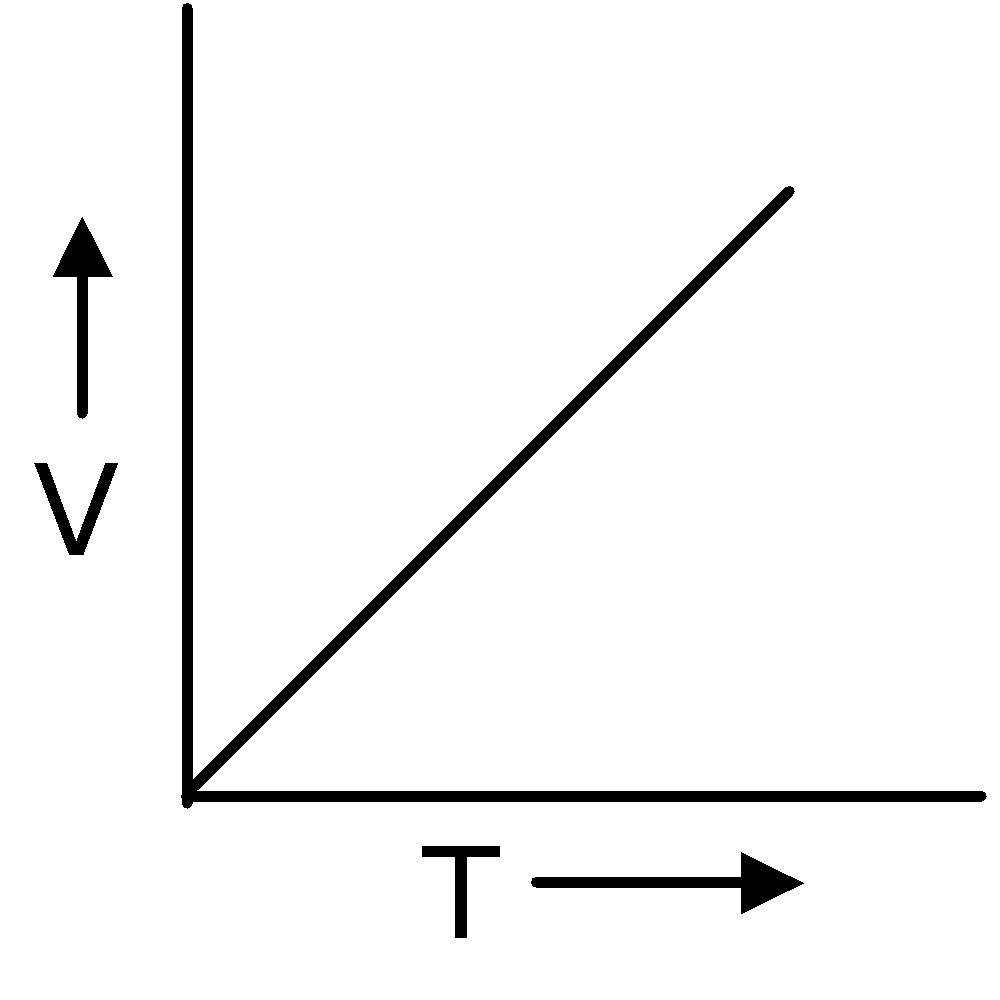
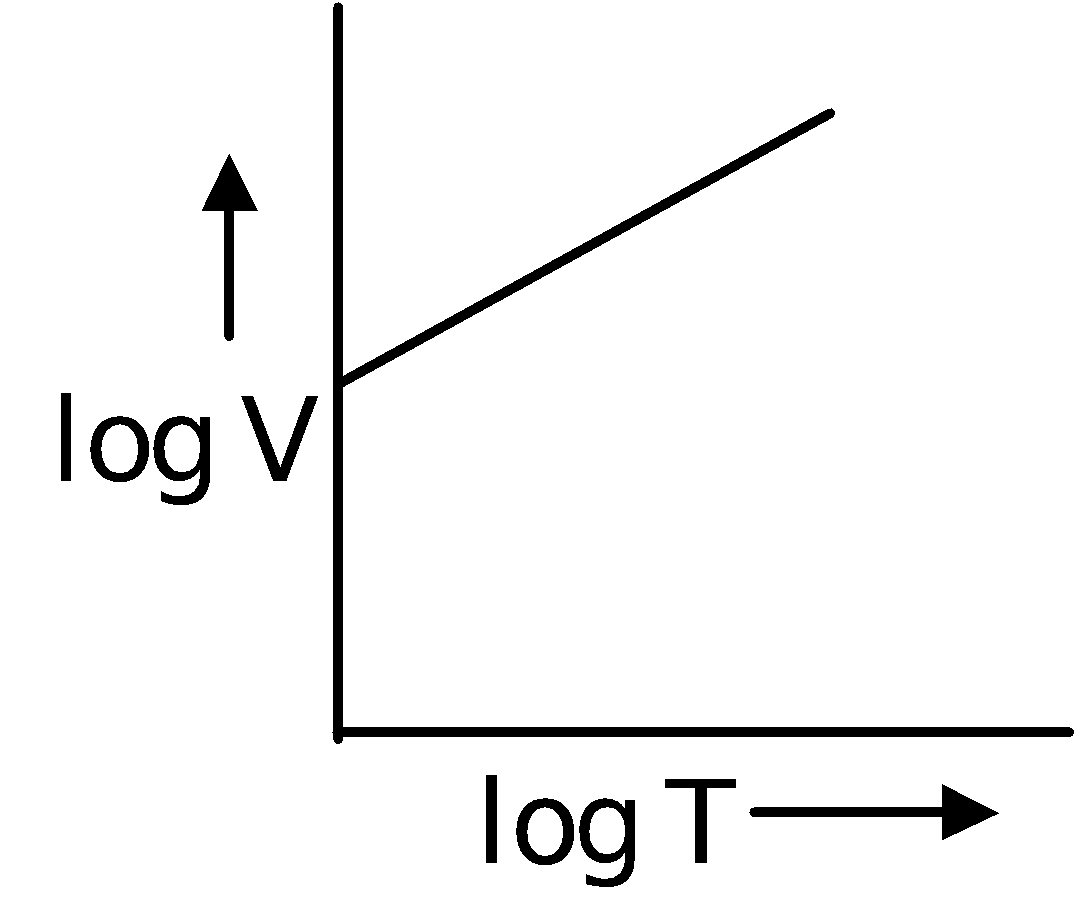
Charles' Law
In 1787, Jacques Charles discovered that if the pressure is kept constant, the volume of a gas sample increases linearly with the temperature for a fixed mass of gas. The unit of temperature used is Kelvin.
∴ V ∝T ( P and n are constant )
∴ 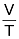 = Constant or
= Constant or 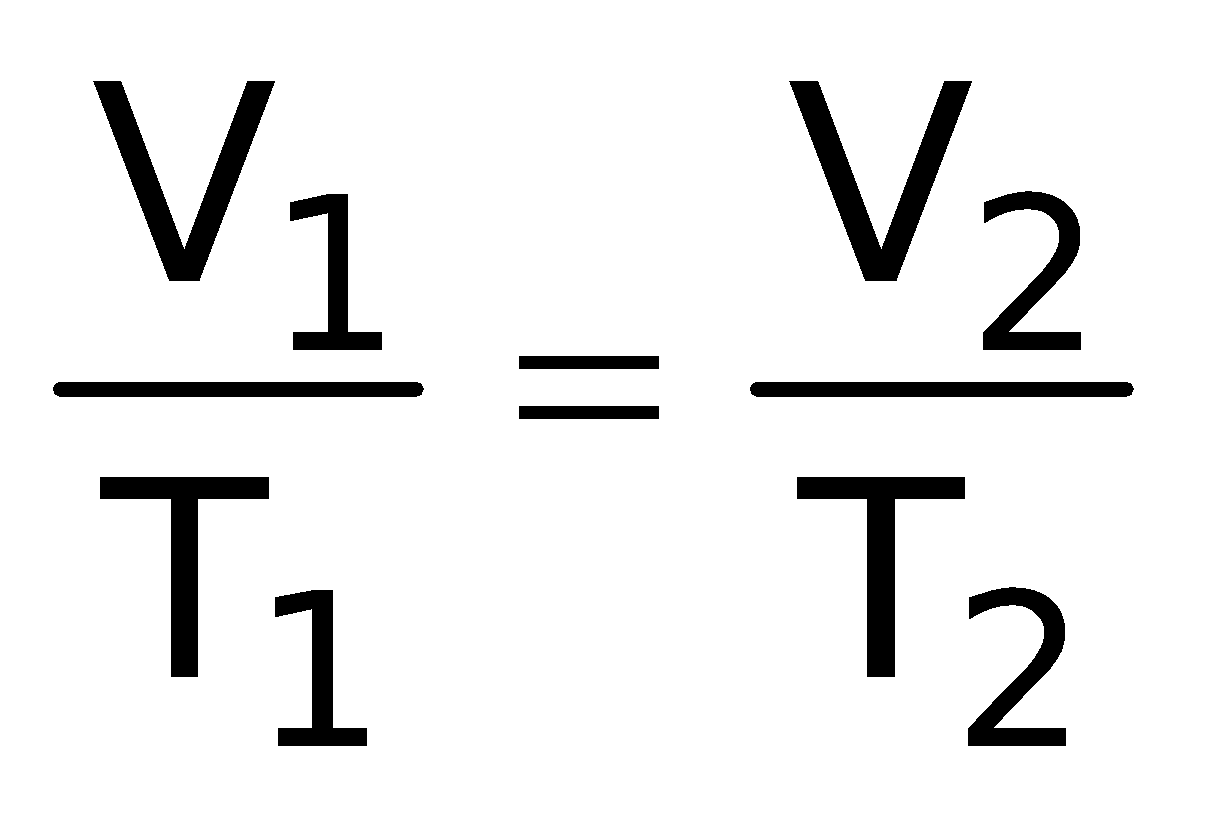
|
(a) |
(b) |
|
Example 2. An open flask contains air at 27ºC. Calculate the fraction of air that would be expelled out, at 477ºC. Solution: Here, gas expands against a constant pressure of 1 atm.
According to Charle’s law. Now, V1 = V (say), T1 = 273 + 27 = 300 K V2= ? T2 = 273 + 477 = 750 K
Thus, volume of air expelled = 2.5 V – V = 1.5 V
Fraction of air expelled =
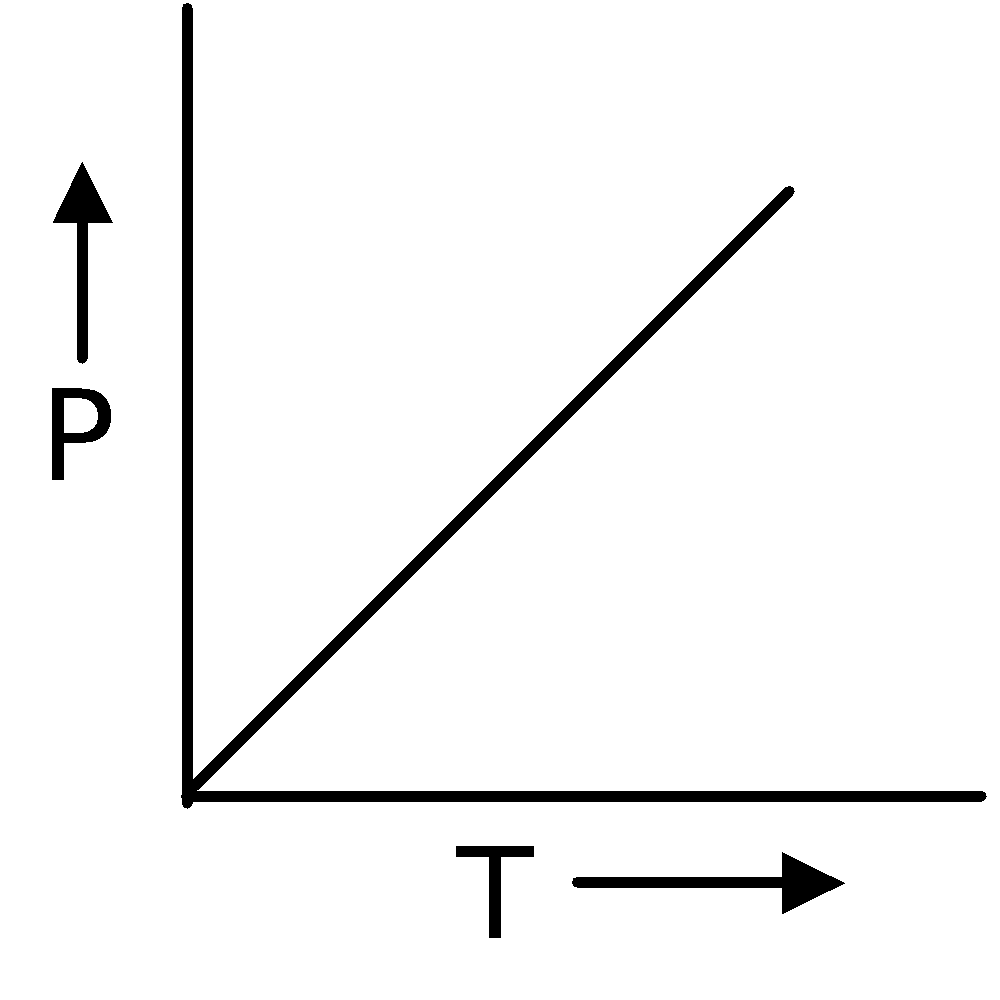
Gay Lussac's LawIn 1802, Gay Lussac discovered that if the volume is kept constant, the pressure of a fixed mass of a gas increases linearly with the rise in temperature. |
|
∴ P ∝T(at constant V and n)
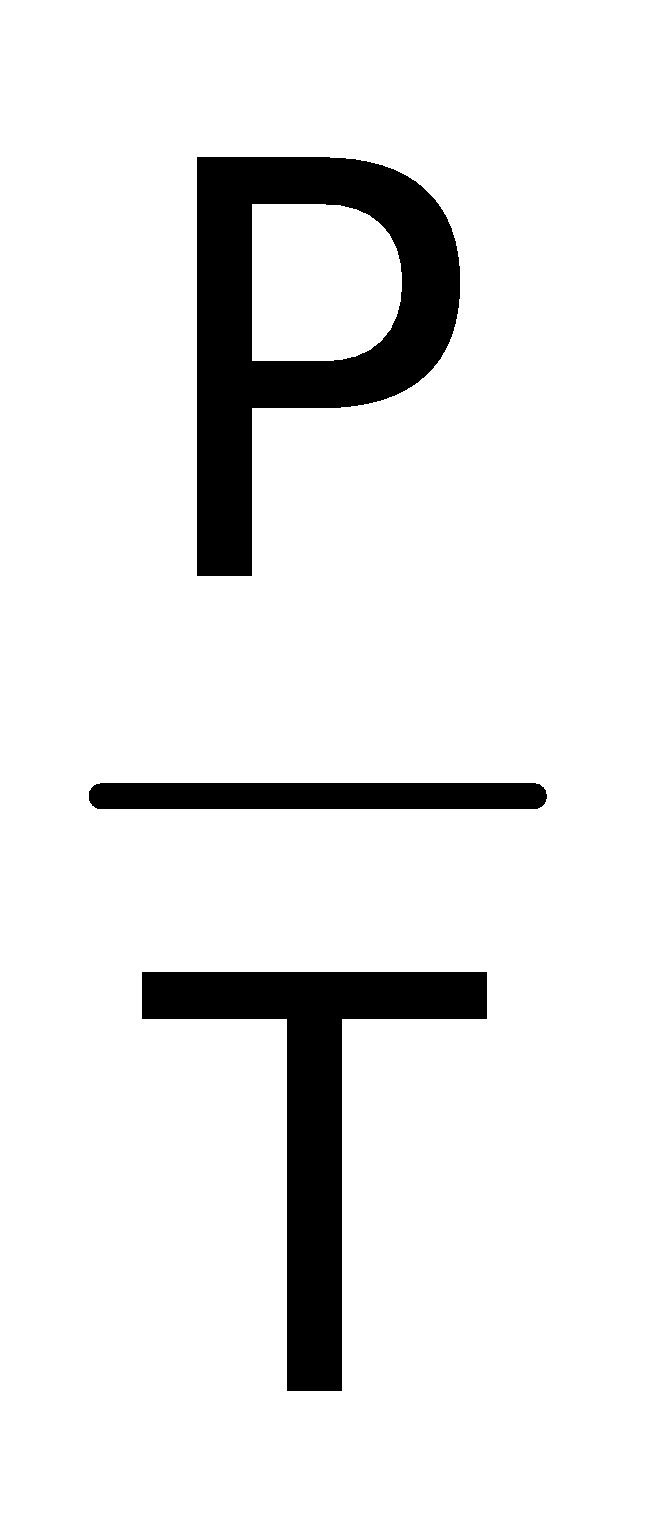 = Constant or
= Constant or 
Example:3 .At 3 atm and 17ºC a gas cylinder has a volume of 10 litre. If the temperature of cylinder is increased to 47ºC, how many liters of air measured at 47ºC and pressure of 1 atm should be let out to restore the pressure to 3 atm at 47ºC ?
Solution: 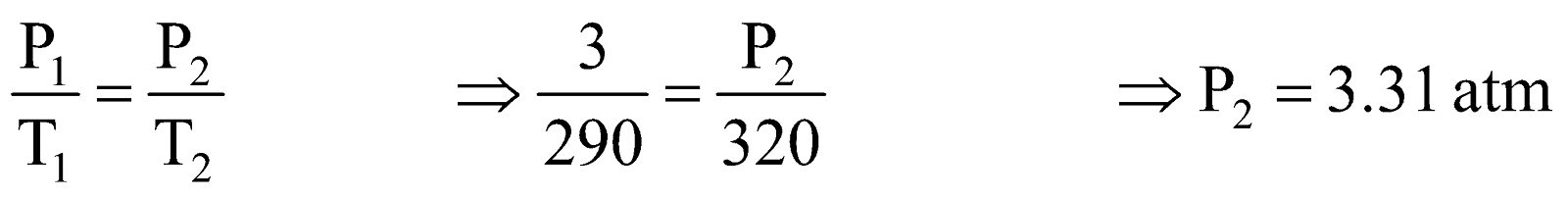 .
.
Pressure to be decreased in cylinder = 3.31 – 3.00 = 0.31 atm.
Let the volume of the gas to be taken out at 1 atm be V. As the temperature remains constant Boyle’s law can be applied to determine V as follows.