Sum of interior angles of a quadrilateral

Understanding quadrilaterals of Class 8

INTERIOR AND EXTERIOR OF A QUADRILATERAL

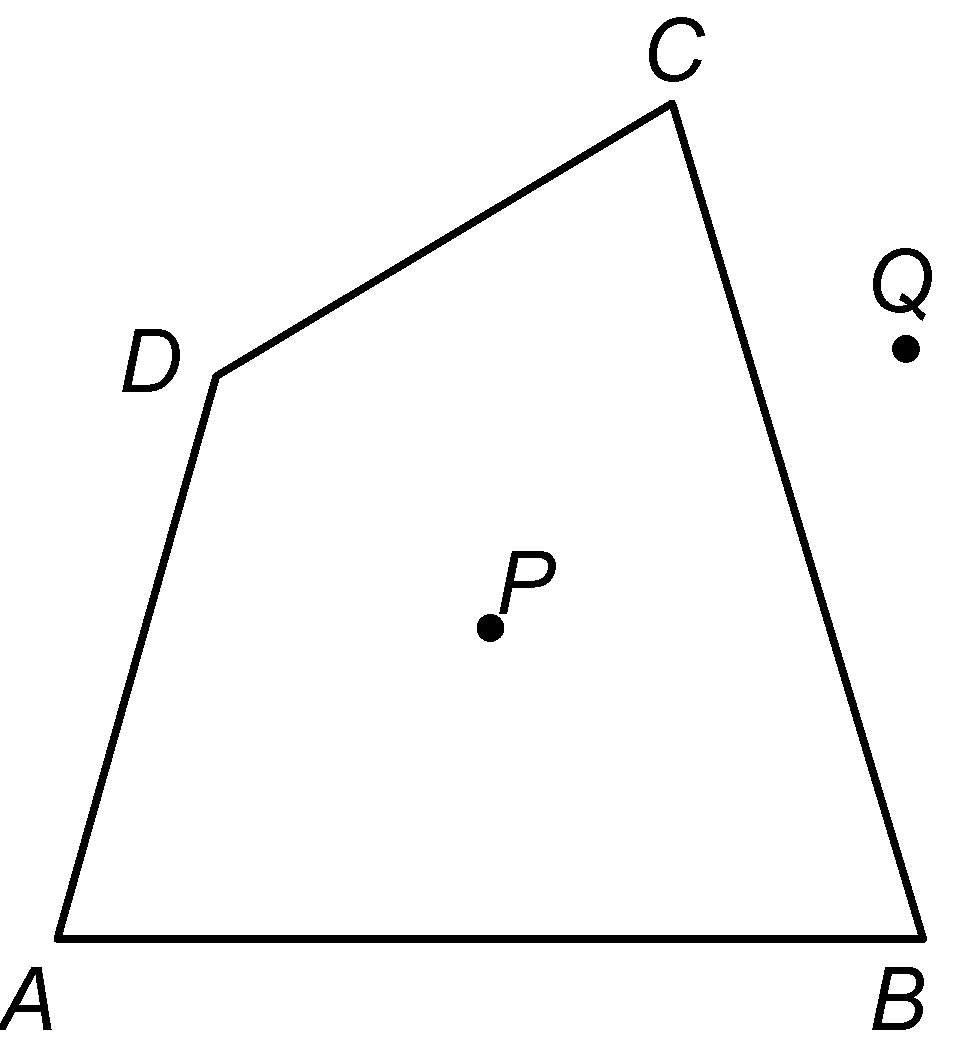
Consider a quadrilateral ABCD. Clearly, it is a plane figure. All points in the plane of quadrilateral ABCD are divided into following three parts:

(i) The part of the plane made up by all such points as are enclosed by quadrilateral ABCD. This part of the plane is called the interior of the quadrilateral ABCD and any point of this part is called an interior point of the quadrilateral.

In figure P is an interior point of quadrilateral ABCD.

(ii) The part of the plane made up by all-points as are not enclosed by the quadrilateral ABCD. This part of the plane is called the exterior of the quadrilateral ABCD and any point of this part is called an exterior point of the quadrilateral.

sum of interior angles of a quadrilateral

(iii) The quadrilateral ABCD itself.

Clearly, quadrilateral ABCD is the boundary of its interior and it separates interior of quadrilateral from its exterior.

QUADRILATERAL REGION:

The interior of a quadrilateral ABCD, together with quadrilateral ABCD, is called the quadrilateral region ABCD.

CONVEX QUADRILATERAL:

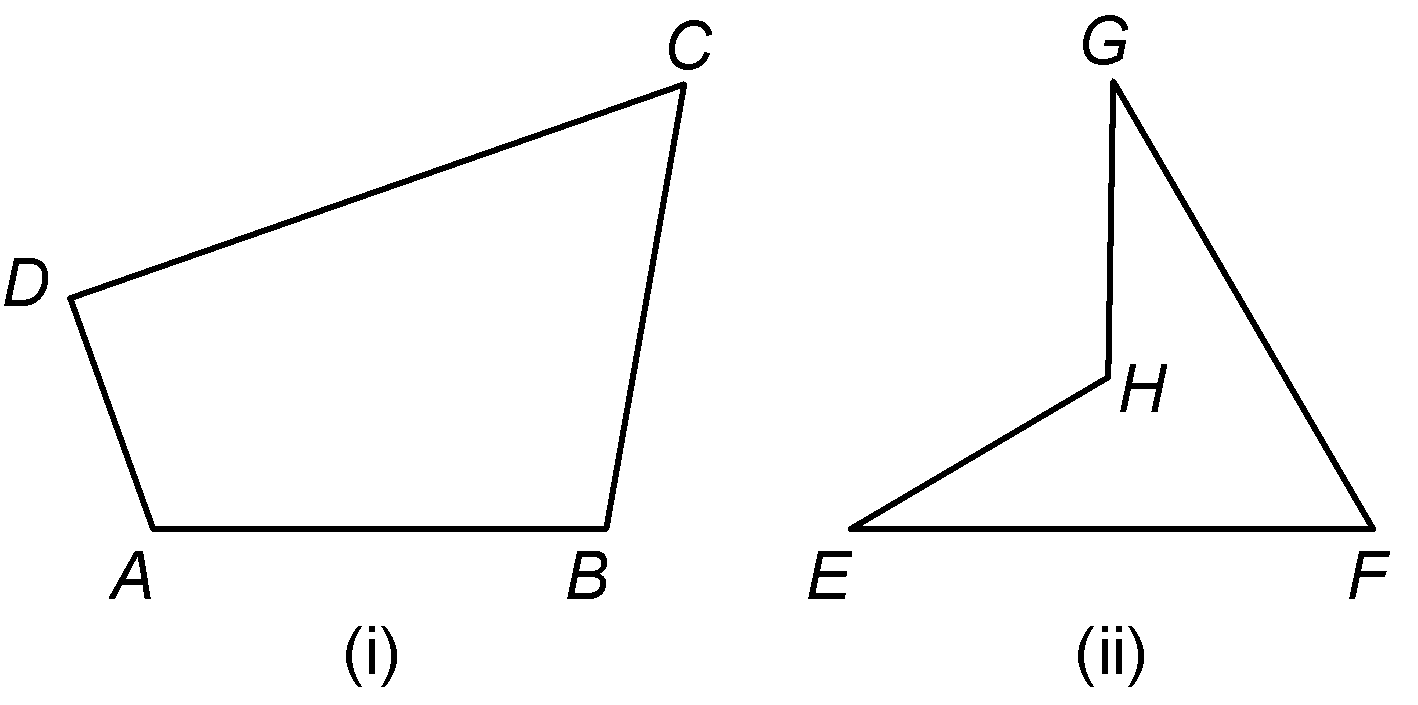
A quadrilateral is called a convex quadrilateral, if the line containing any side of the quadrilateral has the remaining vertices on the same side of it.

In figure (i), quadrilateral ABCD is a convex quadrilateral, because vertices A, B lie on the same side line CD, Vertices B, C lie on the same side of line DA, Vertices C, D lie on the same side of line AB, and Vertices D, A lie on the same side of line BC.

The quadrilateral EFGH shown in figure (ii) is not a convex quadrilateral, because the vertices E and F lie on the opposite side of line GH.