CBSE Class 9 Maths Notes Chapter 8: In Class 9 Math, Chapter 8 talks about Quadrilaterals, which are shapes with four straight sides. This chapter helps you understand different kinds of quadrilaterals, like parallelograms, rectangles, squares, rhombuses, and trapeziums.
You'll learn about their special features and how to recognize them. We'll also explore things like opposite sides and angles, diagonals, and special properties like symmetry and congruence. By understanding this chapter well, you'll be better prepared for more advanced math topics later on.CBSE Class 9 Maths Notes Chapter 8 Quadrilaterals Overview
These notes on Chapter 8, Quadrilaterals, are written by subject experts of Physics Wallah in simple language to help students understand the concepts easily. In this chapter, you will learn about different types of quadrilaterals, such as parallelograms, rectangles, squares, rhombuses, and trapeziums. The notes explain their properties, like the relationships between sides and angles, and how to identify each type of quadrilateral. By studying these notes, students can grasp the fundamentals of quadrilaterals, which will be useful for more advanced math topics in the future.CBSE Class 9 Maths Notes Chapter 8 Quadrilaterals PDF
You can access the CBSE Class 9 Maths Notes for Chapter 8 Quadrilaterals in PDF format using the provided link. These notes provide comprehensive explanations and examples to help you grasp the concepts of triangles effectively.CBSE Class 9 Maths Notes Chapter 8 Quadrilaterals PDF
CBSE Class 9 Maths Notes Chapter 8 Quadrilaterals
Quadrilaterals
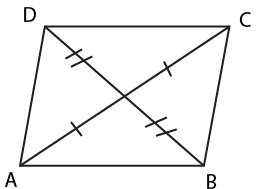
Quadrilaterals are a specific type of polygon characterized by having exactly four sides. These geometric shapes are formed by the union of four line segments. Common examples of quadrilaterals include squares, rectangles, parallelograms, and trapezoids. Each quadrilateral has four vertices (corners) and four angles. The sum of the interior angles of a quadrilateral is always 360 degrees. Understanding the properties and types of quadrilaterals is fundamental in geometry, as they form the basis for more complex shapes and are widely used in various mathematical applications.Examples of Quadrilaterals
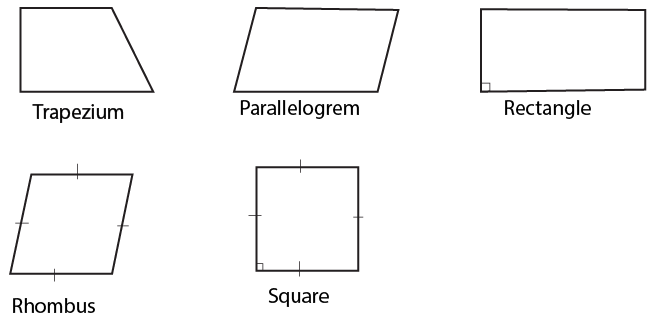
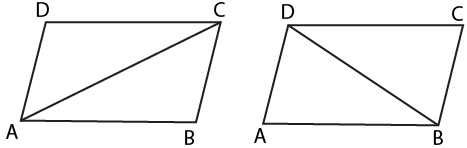
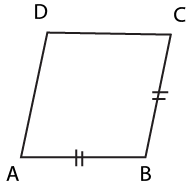
Parallelograms
Sufficient Conditions for a Quadrilateral to be a Parallelogram
CBSE Class 9 Maths Notes Chapter 8 FAQs
What are quadrilaterals?
Quadrilaterals are polygons with four sides. They come in various shapes and sizes, such as squares, rectangles, parallelograms, rhombuses, trapezoids, and kites.
What are the properties of a parallelogram?
Parallelograms have opposite sides that are equal and parallel. Their opposite angles are also equal.
What are the conditions for a quadrilateral to be a parallelogram?
A quadrilateral is a parallelogram if its opposite sides are equal and parallel, or if its diagonals bisect each other, or if one pair of opposite sides are equal and parallel.
How can we calculate the area and perimeter of quadrilaterals?
The area of a quadrilateral can be calculated using various formulas depending on the type of quadrilateral. Perimeter is calculated by adding the lengths of all sides. These calculations are essential in fields such as construction, architecture, and engineering.
🔥 Trending Blogs
Talk to a counsellorHave doubts? Our support team will be happy to assist you!

Check out these Related Articles
Free Learning Resources
PW Books
Notes (Class 10-12)
PW Study Materials
Notes (Class 6-9)
Ncert Solutions
Govt Exams
Class 6th to 12th Online Courses
Govt Job Exams Courses
UPSC Coaching
Defence Exam Coaching
Gate Exam Coaching
Other Exams
Know about Physics Wallah
Physics Wallah is an Indian edtech platform that provides accessible & comprehensive learning experiences to students from Class 6th to postgraduate level. We also provide extensive NCERT solutions, sample paper, NEET, JEE Mains, BITSAT previous year papers & more such resources to students. Physics Wallah also caters to over 3.5 million registered students and over 78 lakh+ Youtube subscribers with 4.8 rating on its app.
We Stand Out because
We provide students with intensive courses with India’s qualified & experienced faculties & mentors. PW strives to make the learning experience comprehensive and accessible for students of all sections of society. We believe in empowering every single student who couldn't dream of a good career in engineering and medical field earlier.
Our Key Focus Areas
Physics Wallah's main focus is to make the learning experience as economical as possible for all students. With our affordable courses like Lakshya, Udaan and Arjuna and many others, we have been able to provide a platform for lakhs of aspirants. From providing Chemistry, Maths, Physics formula to giving e-books of eminent authors like RD Sharma, RS Aggarwal and Lakhmir Singh, PW focuses on every single student's need for preparation.
What Makes Us Different
Physics Wallah strives to develop a comprehensive pedagogical structure for students, where they get a state-of-the-art learning experience with study material and resources. Apart from catering students preparing for JEE Mains and NEET, PW also provides study material for each state board like Uttar Pradesh, Bihar, and others
Copyright © 2025 Physicswallah Limited All rights reserved.
Get App