Angle sum property of quadrilateral
Share
Angle sum property of quadrilateral
Understanding quadrilaterals of Class 8
THEOREM TITLE:
The sum of the angles of a quadrilateral is 360º or 4 right angles.
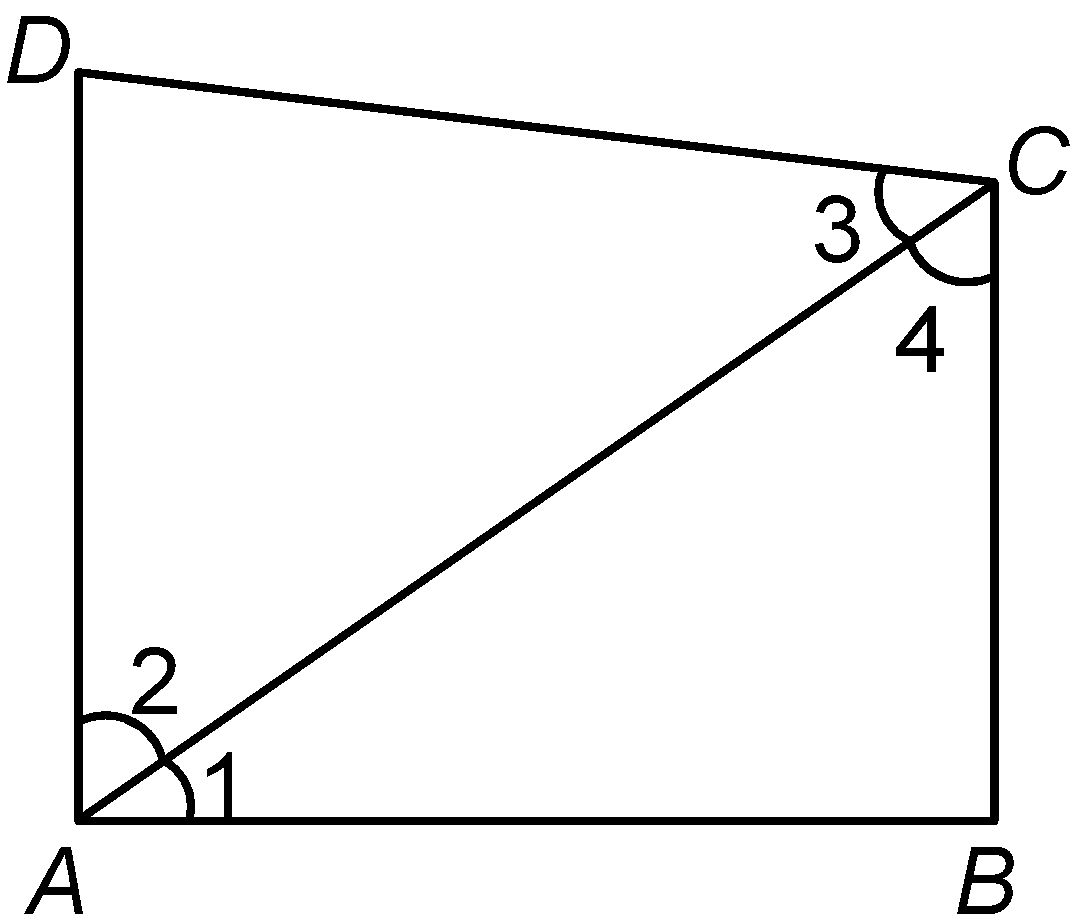
Proof: Let ABCD be a quadrilateral. Draw one of its diagonals, AC.
Clearly, ∠1 + ∠2 = ∠A and ∠3 + ∠4 = ∠C.
We know that the sum of the angles of a triangle is 180º.
|
Therefore, In ΔABC, we have ∠1 + ∠4 + ∠B = 180º ..... (i) And, in ΔACD, we have ∠2 + ∠3 + ∠D = 180º ..... (ii) Adding (i) and (ii), we get (∠1 + ∠4 + ∠B ) + (∠2 + ∠3 + ∠D ) = 180º + 180º ⇒ (∠1 + ∠2) + ∠B + (∠3 + ∠4) + ∠D = 360º |
|
⇒ ∠A + ∠B + ∠C + ∠D = 360º [∠1 + ∠2 = ∠A and ∠3 + ∠4 = ∠C]
THEOREM TITLE:
Prove that the sum of the interior angles of pentagon is 540º.
To prove: ∠A + ∠B + ∠C + ∠D + ∠E = 540º.
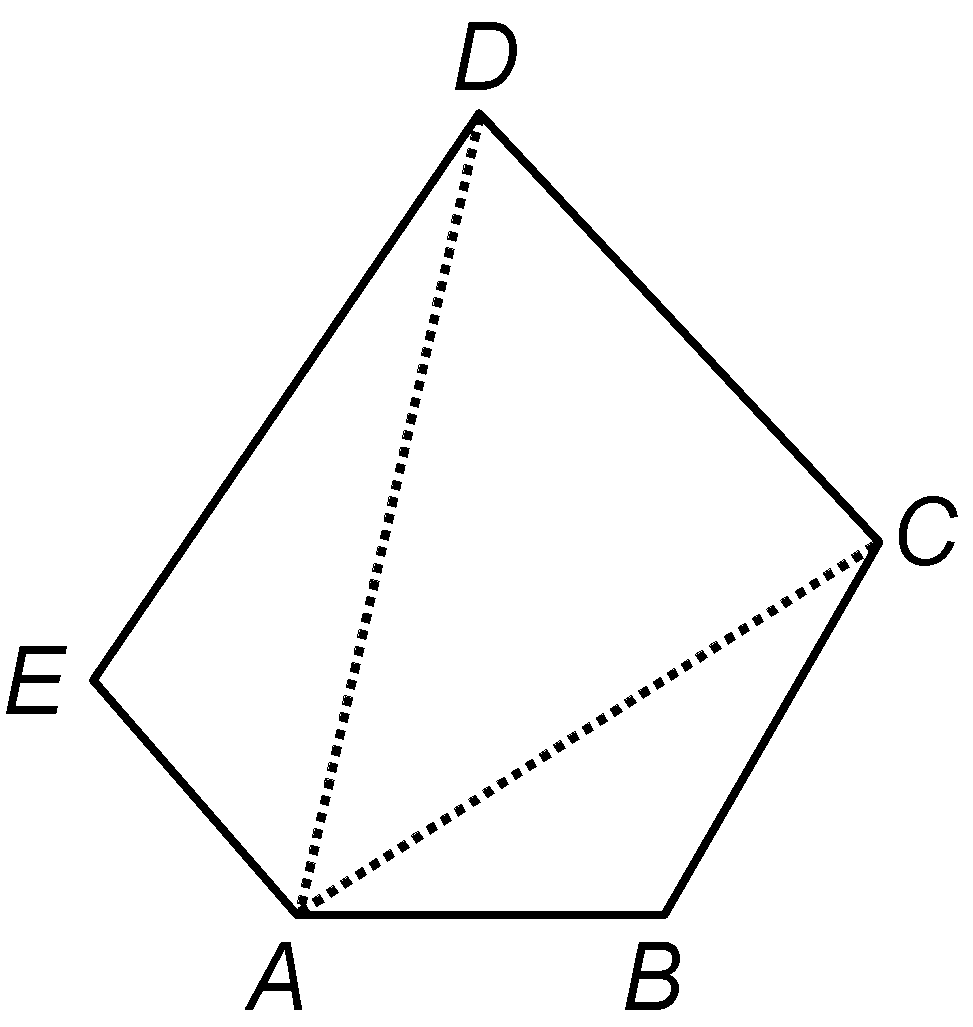
Proof: Let ABCDE be a pentagon. Join AC and AD
We know that the sum of the angles of a triangle is 180º. Therefore, in ΔABC, we have
|
∠BAC + ∠ABC + ∠BCA = 180º ..... (i) Similarly, in triangles ACD and ADE, we have ∠CAD + ∠ACD + ∠ADC = 180º ..... (ii) and, ∠EAD + ∠ADE + ∠DEA = 180º ..... (iii) Adding (i), (ii) and (iii), we get ∠BAC + ∠ABC + ∠BCA + ∠CAD + ∠ACD + ∠ADC + ∠EAD + ∠ADE + ∠DEA = 180º + 180º + 180º ⇒ (∠BAC + ∠CAD + ∠EAD) + ∠ABC + (∠BCA + ∠ACD) + (∠ADC + ∠ADE) + ∠DEA = 540º ⇒ ∠BAE + ∠ABC + ∠BCD + ∠CDE + ∠DEA = 540º ⇒ ∠A + ∠B + ∠C + ∠D + ∠E = 540º |
|
THEOREM TITLE:
Thu sum of all the angles of a hexagon is 720º.
To prove:∠FAB + ∠ABC + ∠BCD + ∠CDE + ∠DEF + ∠EFA = 720º
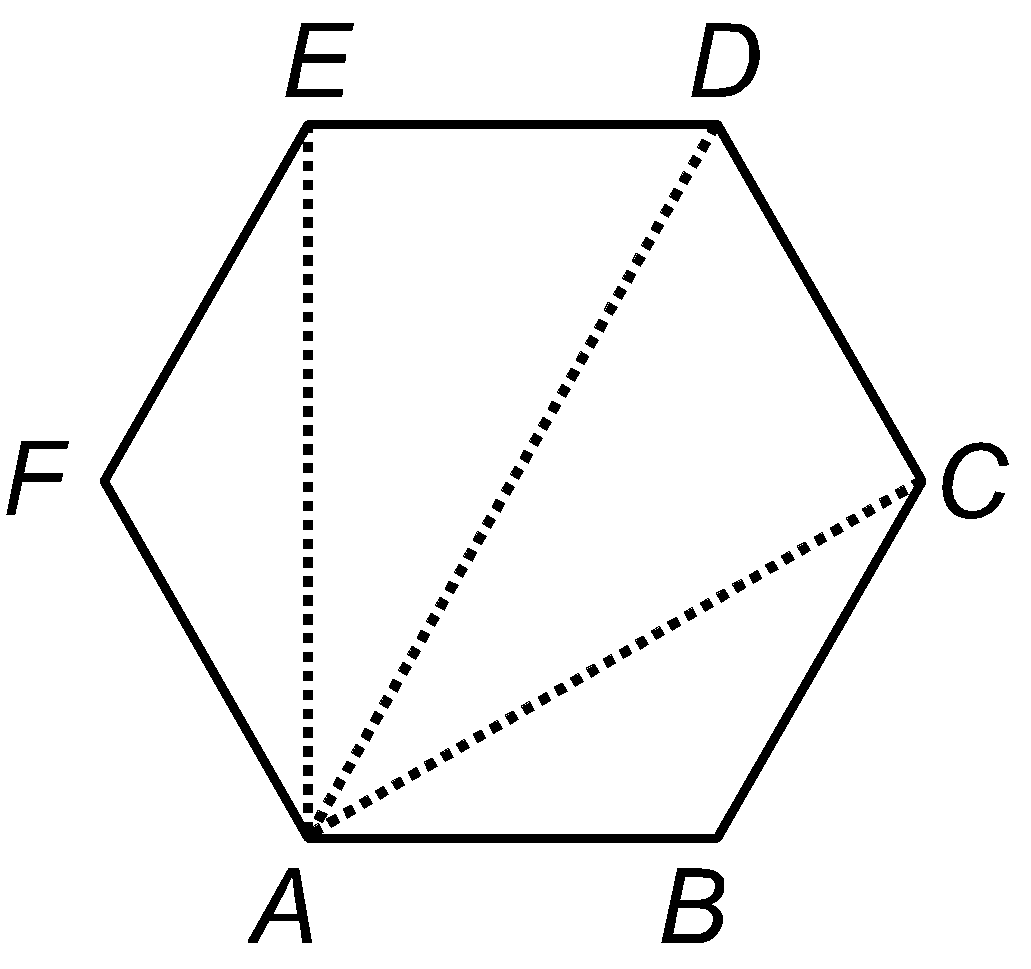
Proof: Let ABCDEF be a hexagon. Join AC, AD and AE.
In ΔABC, we have
|
∠BAC + ∠ABC + ∠BCA = 180º ..... (i) In ΔADC, we have ∠CAD + ∠ADC + ∠ACD = 180º ..... (ii) In ΔADE, we have ∠DAE + ∠ADE + ∠DEA = 180º ..... (iii) In ΔAEF, we have ∠EAF + ∠AEF + ∠AFE = 180º ..... (iv) Adding (i), (ii), (iii), (iv) and regrouping, we get |
|
(∠BAC + ∠CAD + ∠DAE + ∠EAF) + ∠ABC + (∠BCA + ∠ACD) + (∠ADC + ∠ADE)
+ (∠DEA + ∠AEF) + ∠AFE = 720º
⇒ ∠FAB + ∠ABC + ∠BCD + ∠CDE + ∠DEF + ∠EFA = 720º
|
|
|
