SUM OF THE MEASURES OF THE EXTERIOR ANGLES OF A POLYGON
Understanding quadrilaterals of Class 8
THEOREM TITLE:
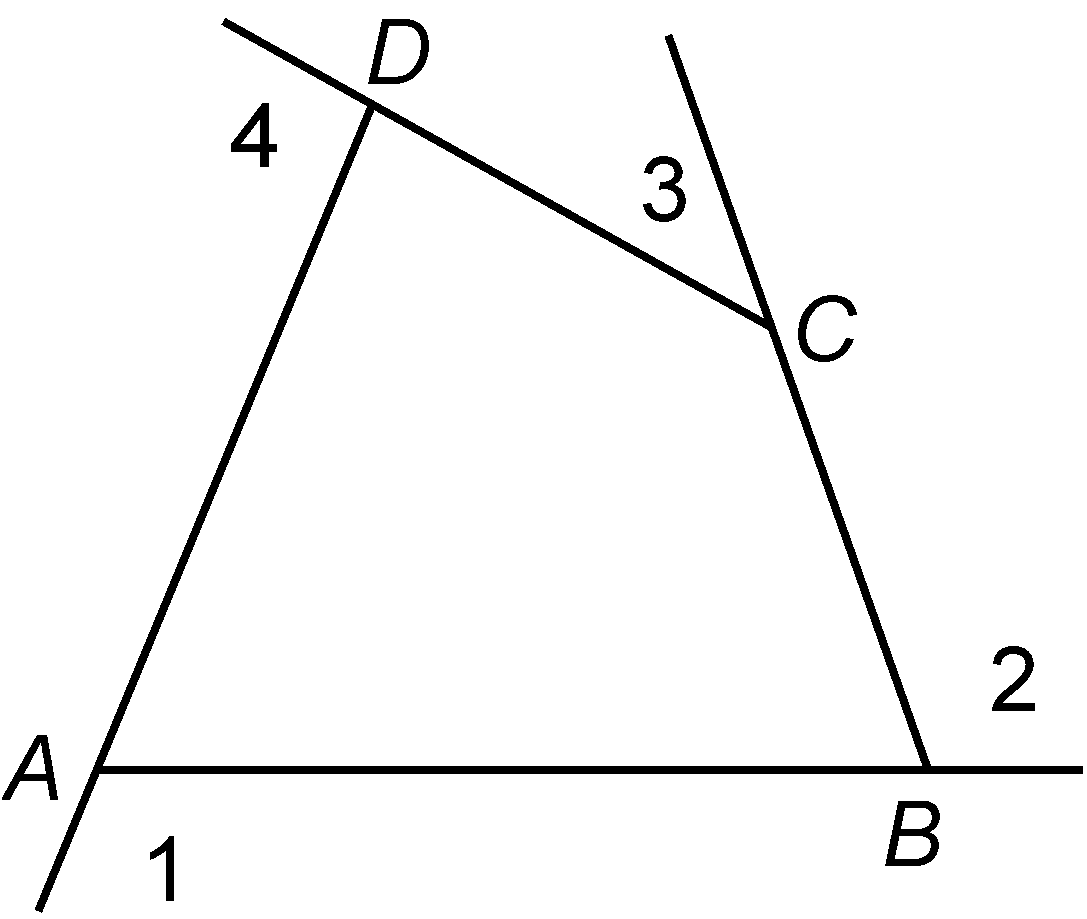
(Exterior angle sum property) If the sides of a quadrilateral are produced in order, the sum of four exterior angles so formed is 360º.
Proof:
Let the sides of a quadrilateral be produced in order as shown in figure, forming exterior angles ∠1, ∠2, ∠3 and ∠4.
Since ∠1 and ∠ form a linear pair and the sum of the angles of a linear pair is 180º.
∴∠1 + ∠A = 180º ----(i)
Similarly, we have
∠2 + ∠B = 180º ----(ii)
∠3 + ∠C = 180º ----(iii)
and, ∠4 + ∠D = 180º ----(iv)
Adding equation (i) to (iv), we have
(∠1 + ∠2 + ∠3 + ∠4) + (∠A + ∠B + ∠C + ∠D) = 180º + 180º + 180º + 180º
⇒ ∠1 + ∠2 + ∠3 + ∠4 + 360º = 720º [∠A + ∠B + ∠C + ∠D = 360º]
→ ∠1 + ∠2 + ∠3 + ∠4 = 720º - 360º = 360º
THEOREM TITLE:
The sum of all the exterior angles formed by producing the sides of a convex polygon in the same order is equal to four right angles.
Given: A convex polygon P1 P2 P3 P4 P5.Its sides P1 P2,P2P3,P3P4, P5P1are produced in order, forming exterior angles ∠1, ∠2, ∠3, ∠4 and ∠5.
To Prove: ∠1 + ∠2 + ∠3 + ∠4 + ∠5 = 4 right angles.
Construction: Take any point O, outside the polygon. Draw OA1,OA2,OA3,OA4, and OA5 parallel to and in the same sense as P1P2,P3P4,P4 P5 and P4 P5, and P5 P1 respectively.
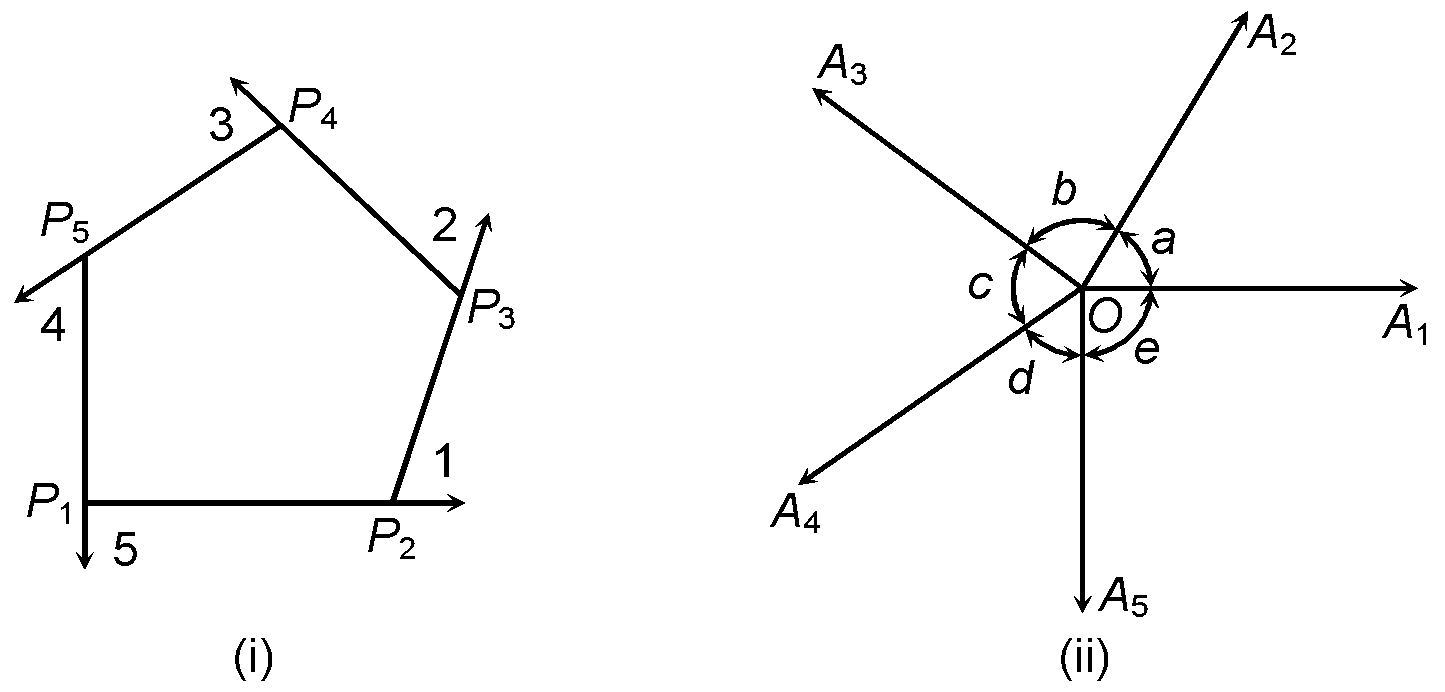
Proof: Since the arms of ∠ and ∠a are parallel and drawn in the same sense. ∴ ∠1 = ∠a
Similarly,∠2 = ∠b, ∠3 = ∠c,∠4 = ∠d and ∠5 = ∠e
∴ ∠1 + ∠2 + ∠3 + ∠4 + ∠5 = ∠a + ∠b + ∠c + ∠d + ∠e = 360º [Sum of the angles at a point is 360º]
= 4 x 90º
= 4 right angles.
 |
➲Each exterior angle of a regular polygon of n sides is equal to 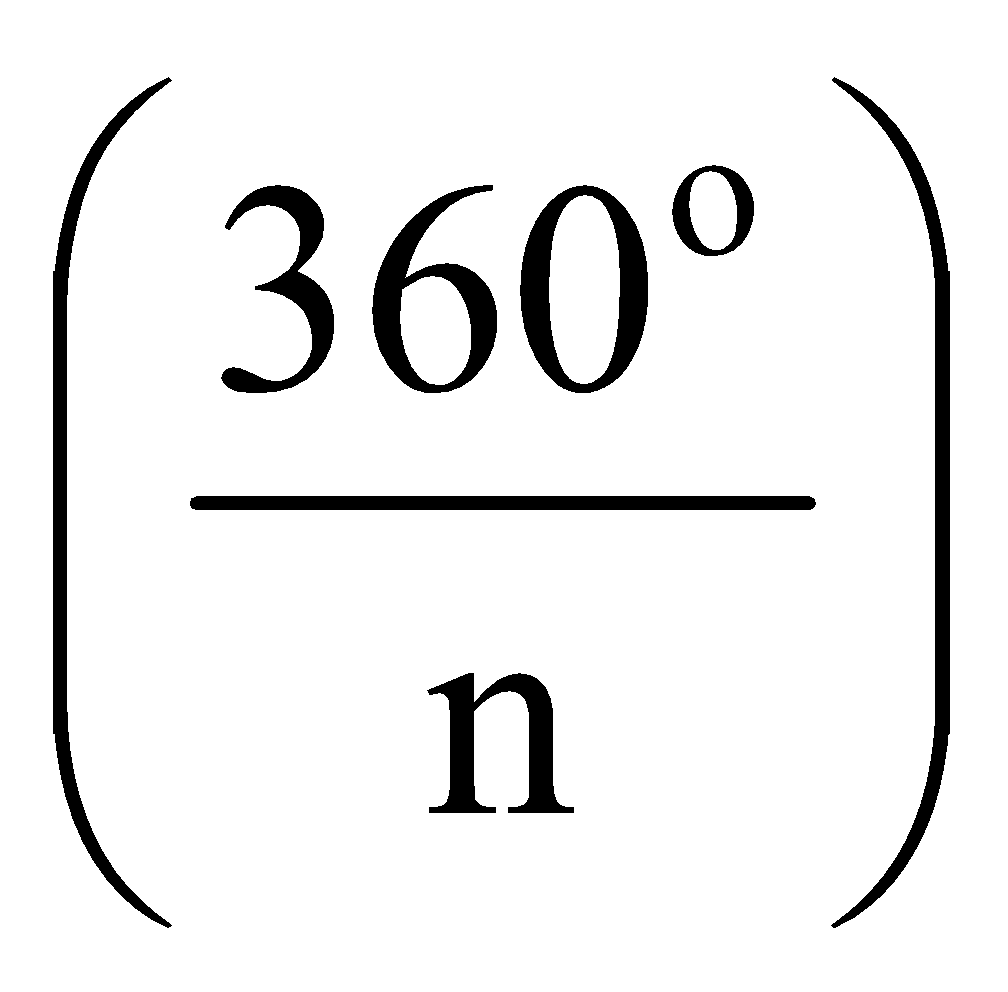 ➲If there is a regular polygon of n sides (n ≥ 3), then its each interior angle is equal to 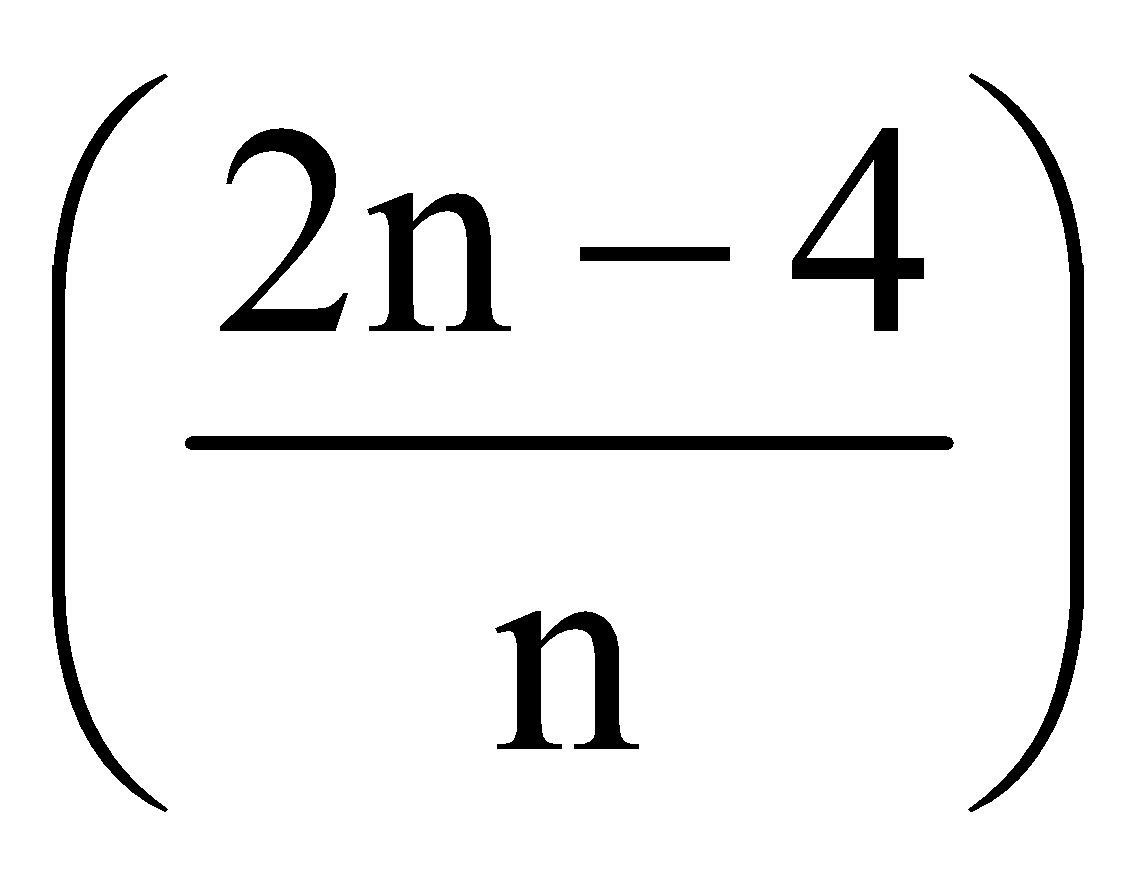 right angles i.e., right angles i.e.,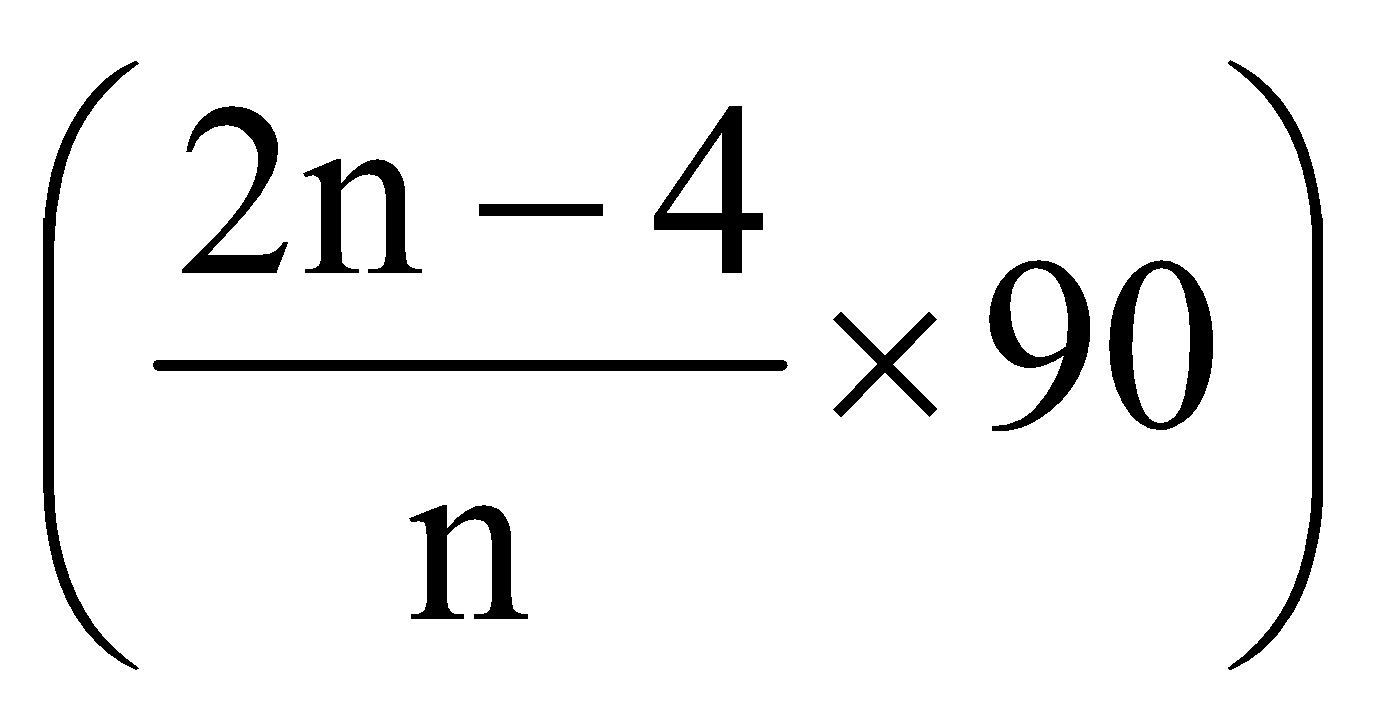 |
- understanding quadrilaterals class 8
- Types of quadrilateral
- Sum of interior angles of a quadrilateral
- Angle sum property of quadrilateral
- SUM OF THE MEASURES OF THE EXTERIOR ANGLES OF A POLYGON
- Parallelogram Definition
- Solved questions on Understanding quadrilaterals
- Exercise 1
- Exercise 2
- Exercise 3 (Fill in the blanks)
- Exercise 4 (True and False)
- Exercise 5









