Implus And Momentum
1. Impulse:
Impulse is the product of the force and the time during which the force acts. If the force is variable, then⇒ The area under F-t graph gives impulse
Momentum: Momentum is directly proportional to the object's mass (m) and velocity (v) The SI unit for momentum is kg m/s. Momentum is so important for understanding motion that it was called the quantity of motion by physicists such as Newton
2. Principle Of Conservation Of Momentum:
The total momentum of a system of particles is a constant in the absence of external forces.
Derivation of Conservation of Momentum
3. Newton's Experimental Law:
The scientific definition of linear momentum is consistent with most people’s intuitive understanding of momentum: a large, fast-moving object has greater momentum than a smaller, slower object. Linear momentum is defined as the product of a system’s mass multiplied by its velocity. In symbols, linear momentum is expressed as p = mv.
Momentum is directly proportional to the object’s mass and also its velocity. Thus the greater an object’s mass or the greater its velocity, the greater its momentum. Momentum p is a vector having the same direction as the velocity v. The SI unit for momentum is kg.m/s.
The efficient of restitution,The Coefficient of Restitution (e) is a variable number with no units, with limits from zero to one.
0 ≤ e ≤ 1
'e' is a consequence of Newton's Experimental Law of Impact, which describes how the speed of separation of two impacting bodies compares with their speed of approach.
note: the speeds are relative speeds
If we consider the speed of individual masses before and after collision, we obtain another useful equation:
uA = initial speed of mass A
uB = initial speed of mass B
vA = final speed of mass A
vB = final speed of mass B
relative initial speed of mass A to mass B = uB - uA
relative final speed of mass A to mass B = vB - vA
![]()
note: in this equation the absolute of uB - uA and vB - vA are used ( |absolute| so there is no net negative result )
4. Analysis Of Collision:
Apply conservation of momentum along the line of collision.
Apply law of restitution along the line of collision
i.e., v2 - v1 = e (u1 - u2)
e = 1 for perfectly elastic collision.
e = 0 for perfectly inelastic collision
0 < e < 1 for other collisions
Elastic collision
If the kinetic energy of the system is conserved during a collision, it is called an elastic collision. (i.e) The total kinetic energy before collision and after collision remains unchanged. The collision between subatomic particles is generally elastic. The collision between two steel or glass balls is nearly elastic. In elastic collision, the linear momentum and kinetic energy of the system are conserved.
Elastic collision in one dimension
If the two bodies after collision move in a straight line, the collision is said to be of one dimension.
Consider two bodies A and B of masses m1 and m2 moving along the same straight line in the same direction with velocities u1 and u2respectively as shown in Fig.. Let us assume that u1 is greater than u2. The bodies A and B suffer a head on collision when they strike and continue to move along the same straight line with velocities v1 and v2 respectively.
From the law of conservation of linear momentum,
Total momentum before collision = Total momentum after collision
m1u1 + m2u2 = m1v1 + m2v2 ...(1)
Since the kinetic energy of the bodies is also conserved during the collision
Total kinetic energy before collision = Total kinetic energy after collision
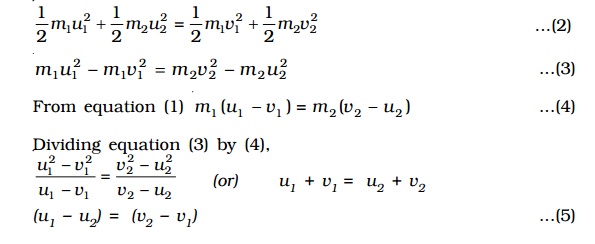
Equation 5 shows that in an elastic one-dimensional collision, the relative velocity with which the two bodies approach each other before collision is equal to the relative velocity with which they recede from each other after collision.
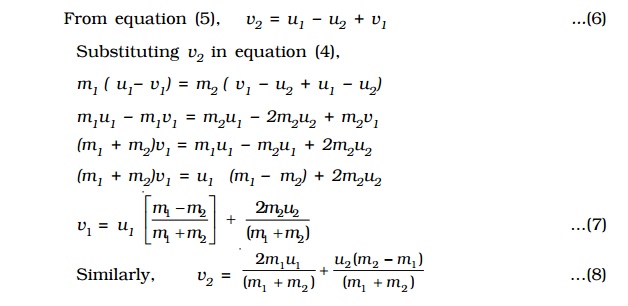
Special cases
Case ( i) : If the masses of colliding bodies are equal, i.e. m1 = m2
v1 = u2 and v2 = u1 .
After head on elastic collision, the velocities of the colliding bodies
are mutually interchanged.
Case (ii) : If the particle B is initially at rest, (i.e) u2 = 0 then
v1 = ( mA-mB / mA+mB) / uA
v2 = ( 2mA / mA+mB) / u1
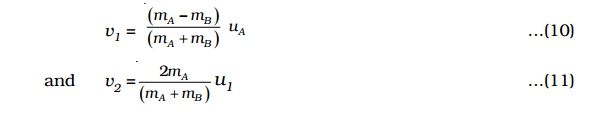
Force due to a jet of water on a wall = u2 Ad, where u is the velocity of the jet, A is the area of cross-section of jet and d is the density of the fluid
In the absence of external forces, the centre of mass of a system has a constant velocity.
Inelastic collision
During a collision between two bodies if there is a loss of kinetic energy, then the collision is said to be an inelastic collision. Since there is always some loss of kinetic energy in any collision, collisions are generally inelastic. In inelastic collision, the linear momentum is conserved but the energy is not conserved. If two bodies stick together, after colliding, the collision is perfectly inelastic but it is a special case of inelastic collision called plastic collision. (eg) a bullet striking a block of wood and being embedded in it. The loss of kinetic energy usually results in the form of heat or sound energy.
Let us consider a simple situation in which the inelastic head on collision between two bodies of masses mA and mB takes place. Let the colliding bodies be initially move with velocities u1 and u2. After collision both bodies stick together and moves with common velocity v.
Total momentum of the system before collision = mAu1 + mBu2
Total momentum of the system after collision =
mass of the composite body ? common velocity = (mA+ mB ) v By law of conservation of momentum
mAu1 + mBu2 = (mA+ mB) v
(or)
v = mAuA + mB uB / mA + mB
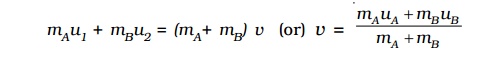
Thus, knowing the masses of the two bodies and their velocities before collision, the common velocity of the system after collision can be calculated.
If the second particle is initially at rest i.e. u2 = 0 then

v = mAuA / (mA+mB)
kinetic energy of the system before collision
EK1 = 1/2 m AuA2 [u2 = 0]
and kinetic energy of the system after collision
EK2 = 1/2(mA +mB )v2
Hence,
Ek2/Ek1 = kinetic energy after collision / kinetic energy before collision
= ( mA+mB)v2 / mAuA2
Substituting the value of v in the above equation,
Ek2/Ek1 = mA/mA+mB
(Or)
Ek2/Ek1 < 1
It is clear from the above equation that in a perfectly inelastic collision, the kinetic energy after impact is less than the kinetic energy before impact. The loss in kinetic energy may appear as heat energy
class="Question_question__2NWpM" id="question-section-id" itemprop="headline" style="box-sizing: border-box; font-family: "Open Sans", sans-serif; -webkit-tap-highlight-color: rgba(255, 255, 255, 0); font-size: 18px; line-height: 1.44; margin-top: unset !important; margin-left: unset !important; margin-right: 10px !important; margin-bottom: 10px !important;"> 5- In the case of rocket propulsion derive expression for:
A) Velocity of rocket at any instant.
B) Thrust on the rocket.
C) Speed of rocket when whole fuel is burnt
The momentum is defined as the product of mass and the velocity. The linear conservation of momentum says that the total momentum of the system is always constant. The impulse is defined as the rate of change of momentum with respect to time.
Formula used:The formula of the momentum is given by,
Where mass is m and velocity is v.
Formula of the force is given by,
Where mass is mass and acceleration is a.









