Rotational Motion

Centre Of Mass Of System Of Particles

(a) The centre of mass (CoM) is the point relative to the system of particles in an object. This is that point of the system of particles that embarks the average position of the system in relation to the mass of the object. At the centre of mass, the weighted mass gives a sum equal to zero. It is the point where any uniform force applied on the object acts.

In other words, a particle’s centre of mass is the point where Newton’s law of motions applies perfectly. When force is applied to the centre of mass, the object as a system of particles moves in the direction of force without rotating. No matter what the shape of the object, the centre of mass helps understand the mechanism of force and motion of that object.      

(b) Two body system

From the equation above we get the centre of mass of two particles with equal masses. From the above equation, it is clear that the CoM of two particles lies in the midway of both.

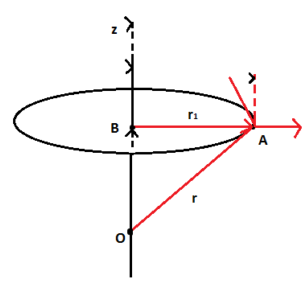
Angular Momentum:

Angular momentum is basically the product of the moment of inertia of an object and its angular velocity. Furthermore, both the quantities must be about the equal and the same axis i.e. the rotation line.

 
       

Torque:

Torque is a twisting force that speaks to the engine's rotational force and measures how much of that twisting force is available when an engine exerts itself. ... This applies torque, or a twisting force, to the bolt.

A simple way to calculate the magnitude of the torque is to first determine the lever arm and then multiply it times the applied force.

Now, from the above observation, we conclude that torque produced depends on the magnitude of the force and the perpendicular distance between the point about which torque is calculated and the point of application of force. So, mathematically torque is represented as:

τ = F.r. sinθ

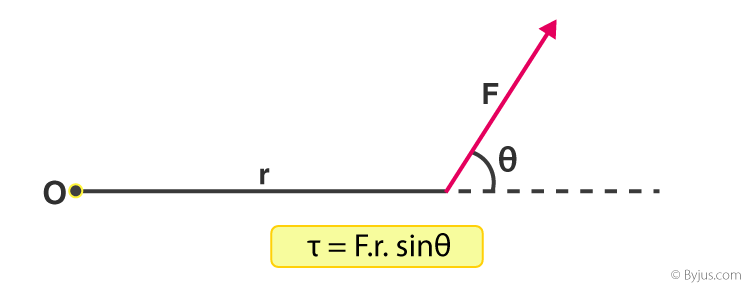
The unit of torque is Newton–meter (N-m). The above equation can be represented as the vector product of force and position vector.

τ = r x F

So, as it is a vector product hence torque also must be a vector. Using vector product notations we can find the direction of torque

Conservation Of Angular Momentum

In the absence of external torque, the angular momentum of a particle does not change.
So rotating objects that collide in a closed system conserve not only linear momentum p in all directions, but also angular momentum L in all directions.

Moment Of Inertia

Moment of inertia is defined as the quantity expressed by the body resisting angular acceleration which is the sum of the product of the mass of every particle with its square of a distance from the axis of rotation. Or in more simple terms, it can be described as a quantity that decides the amount of torque needed for a specific angular acceleration in a rotational axis. Moment of Inertia is also known as the angular mass or rotational inertia. The SI unit of moment of inertia is kg m2.

TABLE: Moment Of Inertia

S.No	Nature of body	Mass	Dimension	Axis	I
1	Uniform solid sphere	M	radius r	Passing through centre of mass
2	Uniform solid cylinder or disc	M	radius r	Coincides with the geometric axis (I,e, longitudinal axis passing through centre of mass)
3	A cylindrical shell or hoop	M	radius r	Coincides with the longitudinal axis passing through the centre of mass	Mr2
4	A thin straight rod	M	Length l	Passing through centre of mass and perpendicular to longitudinal axis
5	A thin straight rod	M	Length 2l	Passing through one of its ends and perpendicular to longitudinal axis.

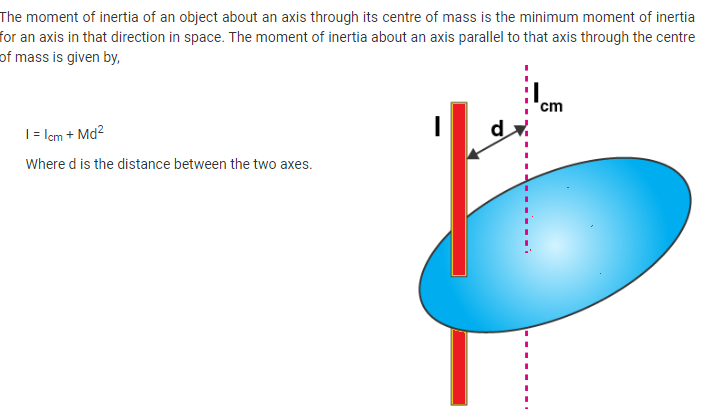
(a) Parallel axes theorem


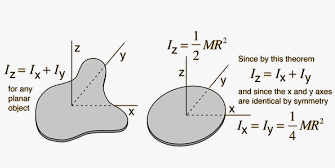
(b) Perpendicular axes theorem

M.O.I of a 2-dimensional object about an axis passing perpendicularly from it is equal to the sum of the M.O.I of the object about 2 mutually perpendicular axes lying in the plane of the object.

According to the above definition of Perpendicular axis theorem can be written as,

IZZ = IXX + IYY

Radius Of Gyration (K):

The moment of inertia of a body about an axis is sometimes represented using the radius of gyration. Now, what do you mean by the radius of gyration? We can define the radius of gyration as the imaginary distance from the centroid at which the area of cross-section is imagined to be focused at a point in order to obtain the same moment of inertia. It is denoted by k.

The formula of moment inertia in terms of the radius of gyration is given as follows:

I = mk2       (1)

where I is the moment of inertia and m is the mass of the body

Accordingly, the radius of gyration is given as follows

k=√Imk=Im(2)

The unit of the radius of gyration is mm. By knowing the radius of gyration, one can find the moment of inertia of any complex body equation (1)  without any hassle.

Consider a body having n number of particles each having a mass of m. Let the perpendicular distance from the axis of rotation be given by r1, r2, r3,…,rn. We know that the moment of inertia in terms of radius of gyration is given by the equation (1). Substituting the values in the equation, we get the moment od inertia of the body as follows

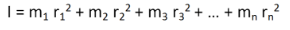
………… (3)

If all the particles have the same mass then equation (3) becomes

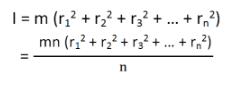
We can write mn as M which signifies the total mass of the body. Now the equation becomes

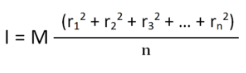
………… (4)

From equation (4), we get

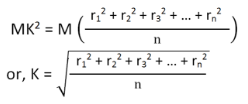
From the above equation, we can infer that the radius of gyration can also be defined as the root-mean-square distance of various particles of the body from the axis of rotation.

Rotatonal Work,Power And Energy

(a) Work done by torque:

Work done is the force multiplied with the distance moved by the force - and can be expressed as

W = F s (1)

where

W = work done (J, Nm)

F = force (N)

s = distance moved by force (s)

For an angular motion

the work done can be expressed as

W = F θ r

= T θ (2)

where

W = work (Joules)

θ = angle (radians)

r = radius (m)

T = torque or moment (Nm)

(b) Power developed by torque

Power is the ratio between the work done and the time taken and can be expressed as

P = W / dt

= T θ / dt

= T ω

= 2 π n T

= 2π (n_rpm / 60) T

= 0.105 n_rpm T(3)

where

P = power (Watts)

dt = time taken (s)

ω =  θ / dt = 2 π n = angular velocity (rad/s)

n = speed (rev/s)

n_rpm = speed (rev/min, rpm)

(c) Kinetic energy of rotation

Things that roll without slipping have some fraction of their energy as translational kinetic and the remainder as rotational kinetic. The ratio depends on the moment of inertia of the object that’s rolling.

Erotational = 12Iω2

where ω is the angular velocity and II is the moment of inertia around the axis of rotation.

The mechanical work applied during rotation is the torque (ττ) times the rotation angle (θ): W=τθ

The instantaneous power of an angularly accelerating body is the torque times the angular velocity: P=τω.

Note the close relationship between the result for rotational energy and the energy held by linear (or translational) motion:

translational=12mv2.In the rotating system, the moment of inertia takes the role of the mass and the angular velocity takes the role of the linear velocity.

As an example, let us calculate the rotational kinetic energy of the Earth (animated in Figure 1 ). As the Earth has a period of about 23.93 hours, it has an angular velocity of 7.29×10⁻⁵ rad/s. The Earth has a moment of inertia, I = 8.04×10³⁷ kg·m2. Therefore, it has a rotational kinetic energy of 2.138×10²⁹ J.

Rolling Motion

(a) In pure rolling (i.e. without slipping):Rolling is a type of motion that combines rotation and translation of that object with respect to a surface, such that, if ideal conditions exist, the two are in contact with each other without sliding. Rolling where there is no sliding is referred to as pure rolling.

Rolling Motion of Disc

(Source: My Rank)

Let us assume that the disc rolls without slipping. If that this disc is the uniform disc the centre of mass lies at the centre of the disc that is the point ‘0’.  The velocity of the centre of mass will always be parallel to the surface as we can see this in the figure.

At any instant of time, there will be two velocities. One is the velocity of the centre of mass and another one is the component of linear velocity. The velocity of the centre of mass is vcm. This corresponds to the translation motion of the object. vr is the linear velocity which corresponds to the rotation.
vr = rω.

Let us first consider the point P0

So at P0 we have two velocities that are vcm and vr. Here the direction of the centre of mass is in the direction of P0andvcm and 

vr are opposite in direction. If we want the object to roll without slipping, the point which is in contact with the ground should be at rest. So vr = vcm

⇒ rω = vcm

(b) Acceleration (a) of a body rolling down on an inclined plane

,

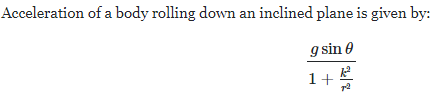where R = radius of body, K = radius of gyration
⇒ Different bodies of same radius such as ring, hollow sphere, solid sphere and cylinder will acquire different accelerations (as they have different K values) and hence take different time to reach the bottom of the plane.