kinematics Notes
Kinematics notes for IIT-JEE
Some Definition Distance: Distance between two points is the length of actual path travelled by the particle. It is a scalar quantity.
Unit : m(metre)
Displacement: Displacement is a vector drawn from the initial position (A) to the final position (B)
Unit : m(metre)
Velocity: Velocity is the rate of change of position vector.
Unit : ms–1 (metre per second)
Acceleration: Acceleration is the rate of change of velocity.
Unit : ms–2 (metre per second2)
Average speed:The average speed of an object can be defined as the total distance travelled by it in a particular interval of time. It can be calculated by dividing the total distance travelled by the total time taken.
average speed (avg) = Total distance covered/ Total time taken
Average velocity: Average velocity is a vector quantity. Average velocity is defined as the change in position or displacement (∆x) divided by the time intervals (∆t) in which the displacement occurs.The average velocity can be positive or negative depending upon the sign of the displacement. The SI unit of average velocity is meters per second (m/s or ms-1)
Average acceleration:
Acceleration is defined as the rate of change of velocity. It is denoted by ‘a’ and is measured in the units of m/s2. For a particular interval, the average acceleration is defined as the change in velocity for that particular interval. Unlike acceleration, the average acceleration is calculated for a given interval.
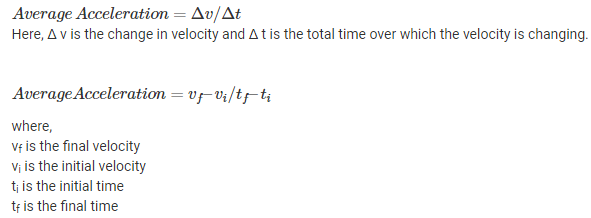
- Uniform velocity: A particle with uniform velocity undergoes equal displacements in equal intervals of time however small the intervals may be.
- Uniform acceleration: A particle with uniform acceleration undergoes equal changes in velocity in equal intervals of time, however small the intervals may be.
GRAPHICAL SOLUTION OF RECTILINEAR MOTION
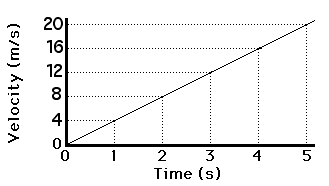
v-t Curve: The area under the v-t curve measures the change in position x.
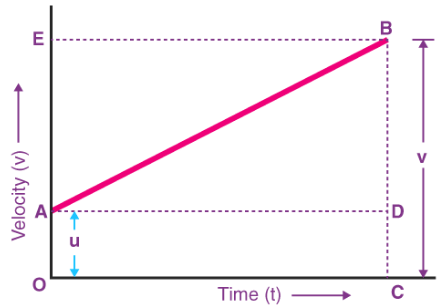
In the above graph,
- The velocity of the body changes from A to B at a uniform rate.
- BC is the final velocity and OC is the total time t.
- A perpendicular is drawn from B to OC, a parallel line is drawn from A to D,and another perpendicular is drawn from B to OE (represented by dotted lines).
Following details are obtained from the graph above:
The initial velocity of the body, u = OA
The final velocity of the body,v = BC
From the graph, we know that
BC = BD + DC
Therefore,v = BD + DC
v = BD + OA (since DC = OA)
Finally,
v = BD + u (since OA = u)(Eqaution 1)
Now, since the slope of a velocity-time graph is equal to acceleration a, So,
a = slope of line AB
a = BD/AD
Since AD = AC = t, the above equation becomes:
BD = at (Equation 2)
Now, combining Equation 1 & 2 , the following is obtained
v=u+at
Derivation of second equation of motion:
Distance travelled (s) = Area of figure OABC = Area of rectangle OADC + Area of triangle ABD
s = (1/2 AB × BD) + (OA × OC)
Since BD = EA, the above equation becomes
s = (1/2 AB × EA) + (u × t)
As EA = at, the equation becomes
s = 1/2 × a × t + ut
Derivation of third equation of motion:

Characteristics of v-t graph: The velocity of an object is its speed in a particular direction. Two cars travelling at the same speed but in opposite directions have different velocities.
A velocity-time graph shows the speed and direction an object travels over a specific period of time. Velocity-time graphs are also called speed-time graphs.
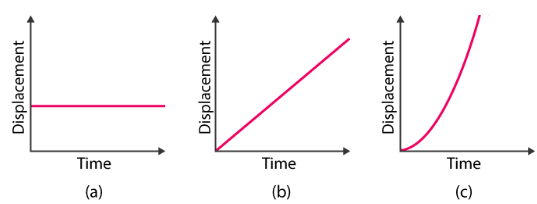
When an object is moving with a constant velocity, the line on the graph is horizontal. When the horizontal line is at zero velocity, the object is at rest. When an object is undergoing constant acceleration, the line on the graph is straight but sloped.
Curved lines on velocity-time graphs also show changes in velocity, but not with a constant acceleration or deceleration. The diagram shows some typical lines on a velocity-time graph.
The steeper the line, the greater the acceleration of the object. The purple line is steeper than the green line because it represents an object with a greater acceleration.Notice that a line sloping downwards - with a negative gradient - represents an object with a constant deceleration (it is slowing down).Acceleration can be calculated by dividing the change in velocity (measured in metres per second) by the time taken for the change (in seconds). The units of acceleration are m/s/s or m/s2
Graphical representation of motion:
- Slope of tangent to position time graph gives velocity.
- Slope of tangent to v−t curve gives acceleration.
- Area enclosed between v−t curve and time axis between an interval of time gives displacement.
- Slope of tangent to a−t curve gives rate of change of acceleration
- Area enclosed between a−t curve and time axis between an interval of time gives change in velocity.
Vectors
Addition of vectors:vector addition is commutative. So, 
It means that the law of addition of vectors is independent of the order of vectors.
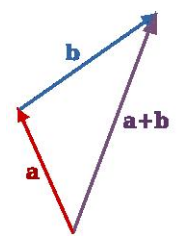
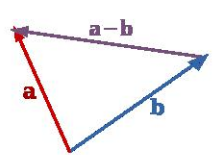
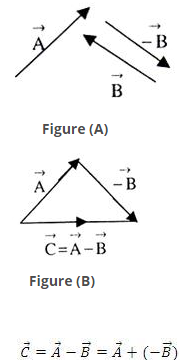
Subtraction of vectors:The process of subtracting one vector from another is equivalent to adding, vectorially, the negative of the vector to be subtracted. Suppose there are two vectors  and
and  , shown in figure (A) and we have to subtract
, shown in figure (A) and we have to subtract 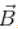 and
and 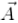 . It is just the same thing as adding vectors –
. It is just the same thing as adding vectors – 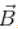 to
to 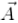 . The resultant is shown in figure (B).
. The resultant is shown in figure (B).
Parallelogram law of vector addition:If two vectors acting at a point are represented in magnitude and direction by the two adjacent sides of a parallelogram, then their resultant is represented in magnitude and direction by the diagonal passing through the common tail of the two vectors.
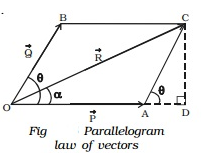
CD is drawn perpendicular to the extended OA, from C. Let COD made by Vec R with Vec P be α.
From right angled triangle OCD,
OC2 = OD2 + CD2
= (OA + AD)2 + CD2
= OA2 + AD2 + 2.OA.AD + CD2 .....(1)
In Fig. Angle BOA = θ =Angle CAD
From right angled ∆ CAD,
AC2 = AD2 + CD2 ...(2)
Substituting (2) in (1)
OC2 = OA2 + AC2 + 2OA.AD ...(3)
From ∆ACD,
CD = AC sin θ ...(4)
AD = AC cos θ ...(5)
Substituting (5) in (3) OC2 = OA2 + AC2 + 2 OA.AC cos θ
Substituting OC = R, OA = P,
OB = AC = Q in the above equation
R2 = P2 + Q2 + 2PQ cos θ(or)
R = root [ P2 + Q2 + 2PQ cos θ ] ...(6)
Equation (6) gives the magnitude of the resultant. From ∆ OCD,
tan α = CD / OD = CD/( OA +AD )
Substituting (4) and (5) in the above equation,
tan α = ( AC sin θ ) / (OA + AC cos θ )
(or) α = tan-1[Qsin θ / (P+Qcos θ)] ...(7)
Equation (7) gives the direction of the resultant

Special Cases
-
When two vectors act in the same direction
In this case, the angle between the two vectors θ = 0o, cos 0o = 1, sin 0o=
From (6)
R = root [ P2 + Q2 + 2PQ ] = P+Q
From (7)
α = tan-1[Qsin 00 / (P+Qcos 00)] (i.e) =0
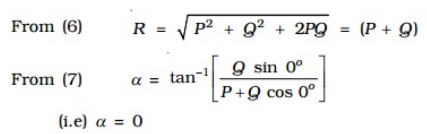
Thus, the resultant vector acts in the same direction as the individual vectors and is equal to the sum of the magnitude of the two vectors. -
When two vectors act in the opposite direction
In this case, the angle between the two vectors θ = 180o, cos 180o = -1, sin 180o= 0.
From (6)
R = root [ P2+ Q2- 2PQ ] = P-Q
From (7)
α = tan-1[Q / (P-Q)] (i.e) =0
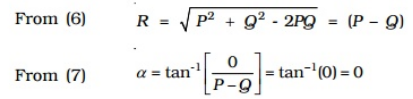
Thus, the resultant vector has a magnitude equal to the difference in magnitude of the two vectors and acts in the direction of the bigger of the two vectors -
When two vectors are at right angles to each other In this case,&theta= 900o, cos 90o = 0,sin 90o= 1
From (6) R=root(P2+Q2)
From (7) a=tan-1(Q/P)
The resultant Vector R vector acts at an angle α with vector Vector P.
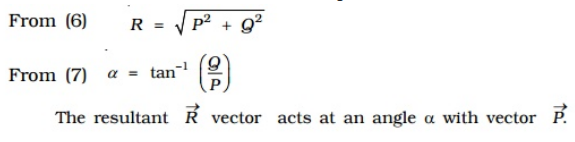
Relative Velocity: Relative velocity is used to denote the aircraft moving in the wind or boats moving through the water, etc. The velocity is measured within the object according to the observer. It can be measured using the use of an intermediate reference frame. In simpler terms, this can be the vector sum of the velocities. The relative velocity formula is expressed as
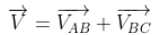
Where VABis the velocity with respect to A and B, VBC is the velocity with respect to B and C and V AC is the velocity with respect to A and C.Let us consider two objects, A and B moving with velocities Va and Vb with respect to a common stationary frame of reference, say the ground, a bridge or a fixed platform.
The velocity of the object A relative to the object B can be given as,
Vab = Va - Vb
Similarly, the velocity of the object B relative to that of object a is given by,
Vba = Vb - Va
From the above two expressions, we can see that
Vab = -Vba
Although the magnitude of both the relative velocities is equal to each other. Mathematically,
|Vab| = |Vba|
Resolution of vectors: The component of F in a direction making an angle θ is F cos θ.
The other component of F at right angles to F cos θ is F sin θ.
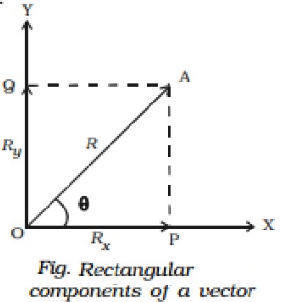
A vector directed at an angle with the co-ordinate axis, can be resolved into its components along the axes. This process of splitting a vector into its components is known as resolution of a vector.
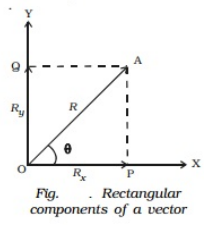
Consider a vector R = Vector( OA) making an angle θ with X - axis. The vector R can be resolved into two components along X - axis and Y-axis respectively. Draw two perpendiculars from A to X and Y axes respectively. The intercepts on these axes are called the scalar components Rx and Ry.
Then, OP is Rx, which is the magnitude of x component of Vector R and OQ is Ry, which is the magnitude of y component of Vector R.
From ∆ OPA,
cos θ = OP/OA = Rx/R(or) Rx=Rcos θ
sin θ = OQ/OA = Ry/R (or) Ry=Rsin θ
R2 = Rx2 + Ry2
Also, Vector R can be expressed as Vector R = Rxi + Ryj where i and j are unit vectors.
In terms of Rx and Ry , θ can be expressed as θ = tan−1 [Ry/Rx]
Unit vector: A vector having unit magnitude is called a unit vector. It is also defined as a vector divided by its own magnitude. A unit vector in the direction of a vector A ![]() ,is written as  and is read as 'A cap' or 'A caret' or 'A hat'. Therefore,
,is written as  and is read as 'A cap' or 'A caret' or 'A hat'. Therefore,
.png)
Thus, a vector can be written as the product of its magnitude and unit vector along its direction.
Dot product:
The geometric meaning of dot product says that the dot product between two given vectors and bis denoted by:
a⋅b = a ∣∣ b ∣ cos
Here, |a| and |b| are called as the magnitudes of vector a and b and θ is the angle between the vectors a and b.
If the two vectors are orthogonal, that is, the angle between them is 90, then a.b = 0 since cos 90 = 0.
If the two vectors are parallel to each other, then a.b =|a||b| since cos 0 = 1.
Dot Product Algebra Definition
The dot product algebra says that the dot product of the given two products - a = (a1,a2,a3,) and b = (b1,b2,b3)is given by:
a.b = (a1b1 + a2b2 + a3b3)
Dot Product of Two Vectors Properties
Given below are the properties of vectors:
-
Commutative Property
a .b = b.a
a.b =|a| b|cos θ
a.b =|b||a|cos θ -
Distributive Property
a.(b + c) = a.b + a.c -
Bilinear Property
a.(rb + c) = r.(a.b) + (a.c) -
Scalar Multiplication Property
(xa) . (yb) = xy (a.b) -
Non-Associative Property
Since the dot product between a scalar and a vector is not allowed -
Orthogonal Property
Two vectors are orthogonal only when a.b = 0
Vector product or Cross product
The vector product or cross product of two vectors A and B is denoted by , A x B, and its resultant vector is perpendicular to the vectors A and B.The cross product is mostly used to determine the vector, which is perpendicular to the plane surface spanned by two vectors, whereas the dot product is used to find the angle between two vectors or the length of the vector. The cross product of two vectors, say A x B,is equal to another vector at right angles to both, and it happens in the three-dimensions.
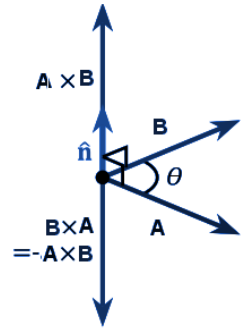
If θ is the angle between the given two vectors A and B, then the formula for the cross product of vectors is given by:
A x B = |A| |B| sin θ
Or, Vector A x Vector B = ||Vector A || ||Vector B|| sin θn^
Here, Vector A, Vector B are two Vectors.
||Vector A || ||Vector B|| are the magnitudes of given vectors.
θ is the angle between two vectors and n^is the unit vector perpendicular to the plane containing the given two vectors, in the direction given by the right-hand rule.
Cross product of two vectors Formula
Consider two vectors,
A = ai + bj + ck
B = xi + yj + zk
We know that the standard basis vectors i,j and k satisfy the below-given equalities.
i x j = k and j x i = -k
j x k = i and k x j = -i
k x i = j and i x k = -j
Also, the anti-commutativity of the cross product and the distinct absence of linear independence of these vectors signifies that:
i x i = j x j = k x k = 0
Now,
A × B = (ai + bj + ck) × (xi + yj + zk) = ax(i × i) + ay(i × j) + az(i × k) + bx(j × i) + by(j × j) + bz(j × k) + cx(k × i) + cy(k × j) + cz(k × k)
By applying the above mentioned equalities,
A × B = ax(0) + ay(k) + az(-j) + bx(-k) + by(0) + bz(i) + cx(j) + cy(-i) + cz(0) = (bz – cy)i + (cx – az)j + (ay – bx)k
Cross product matrix:
We can also derive the formula for the cross product of two vectors using the determinant of the matrix as given below.
A = ai + bj + ck B = xi + yj + zk
Thus,
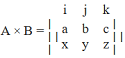
A × B = (bz – cy)i – (az – cx)j + (ay – bx)k = (bz – cy)i + (cx – az)j + (ay – bx)k
Cross product of perpendicular Vector:
Cross product of two vectors is equal to the product of their magnitude, which represents the area of a rectangle with sides X and Y. If two vectors are perpendicular to each other, then the cross product formula becomes:
θ= 90 °
We know that, sin 90° = 1
So,

Cross Product of parallel vector:
The cross product of two vectors are zero vectors if both the vectors are parallel or opposite to each other. Conversely, if two vectors are parallel or opposite to each other, then their product is a zero vector. Two vectors have the same sense of direction.
θ= 90 degrees
As we know, sin 0° = 0 and sin 90° = 1
So,

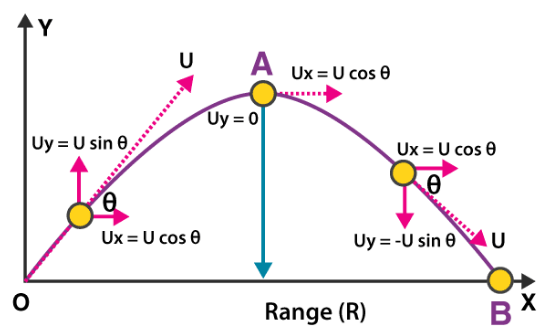
Projectile Motion : When a particle is thrown obliquely near the earth’s surface, it moves along a curved path under constant acceleration that is directed towards the centre of the earth (we assume that the particle remains close to the surface of the earth). The path of such a particle is called a projectile and the motion is called projectile motion.
In a Projectile Motion, there are two simultaneous independent rectilinear motions:
Total Time of Flight: Resultant displacement (s) = 0 in Vertical direction. Therefore, by using the Equation of motion:
gt2 = 2(uyt – sy) [Here,uy = u sin θ and sy = 0]
i.e. gt2 = 2t × u sin θ
- Along the x-axis: uniform velocity, responsible for the horizontal (forward) motion of the particle.
- Along y-axis: uniform acceleration, responsible for the vertical (downwards) motion of the particle.
- First Equation of Motion: v = u + at
- Second Equation of Motion: s = ut + 1/2 at2
- Third Equation of Motion: v2 = u2 + 2as
Time of flight :

Horizontal range:
Horizontal Range (OA) = Horizontal component of velocity (ux) × Total Flight Time (t)
R = u cos θ × 2u×sinθg
Therefore, in a projectile motion the Horizontal Range is given by (R):
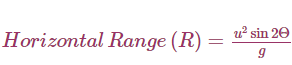
Maximum horizontal range

Projectile on inclined plane:
Let the particle strike the plane at A so that OA is the range of the projectile on inclined plane. This initial velocity 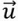 can be resolved into two components:
can be resolved into two components:
- g sin β parallel to the plane
- g cos β perpendicular to the plane.
Time of Flight:- Let t be the time taken by the particle to go from A to B. In this time the displacement of the projectile to the plane is zero.
Hence, 0 = u sin (α-β) t - ½g β t2
=> t = 2u sin(α-β)/gcosβ
Range:-
During time of flight, the horizontal velocity u cos α remains constant.
Hence, horizontal distance,
OB = (ucosα) t = 2u2sin(α-β)cosα/gcosβ
Now, OA = OB/cosβ = 2u2sin(α-β)cosα/gcosβ
The greatest distance of the projectile from the inclined plane is u2sin2 (α-β)/2gcosβ .
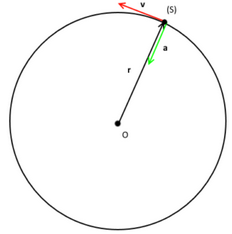
Circular Motion:
Circular motion is the movement of an object in a circular path.
-
Uniform circular motion:
motion refers to the circular motion if the magnitude of the velocity of the particle in circular motion remains constant. The non-uniform circular motion refers to the circular motion when the magnitude of the velocity of the object is not constant. Another special kind of circular motion is when an object rotates around itself also known by spinning motion.
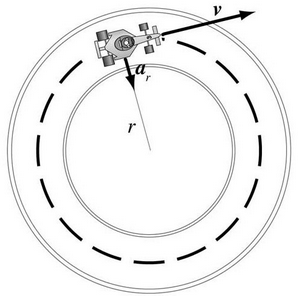
- Variables in Circular Motion
-
Angular Displacement The angle which is subtended by the position vector at the center of the circular path refers to the angular displacement.
Angular Displacement (Δθ) = (ΔS/r)
Where Δ’s refers to the linear displacement while r is the radius. Radian is the unit of Angular Displacement. -
Angular Acceleration
It refers to the rate of time of change of angular velocity (dῶ).
Angular acceleration (α) = dῶ/dt = d2θ / dt2
Its unit is rad/s2and dimensional formula [T]-2. The relation between linear acceleration (a) and angular acceleration (α)
A = rα, where r is the radius. -
Angular Velocity
It refers to the time rate change of angular displacement (dῶ).
Angular Velocity (ῶ) = Δθ/Δt
Angular Velocity is a vector quantity. Its unit is rad/s. The relation between the linear velocity (v) and angular velocity (ῶ) is v = rῶ -
Centripetal Acceleration
It refers to an acceleration that acts on the body in circular motion whose direction is always towards the center of the path.
Centripetal Acceleration (α) = v2/r = rῶ2.
The magnitude of this acceleration by comparing ratios of velocity and position around the circle. Since the particle is traveling in a circular path, the ratio of the change in velocity to velocity will be the same as the ratio of the change in position to position. It is also known as radial acceleration as it acts along the radius of the circle. Centripetal Acceleration is a vector quantity and the unit is in m/s2. -
Non-uniform circular motion:
A change in speed means that unequal length of arc (s) is covered in equal time intervals. It further means that the change in the velocity (v) of the particle is not limited to change in direction as in the case of uniform circular motion. In other words, the magnitude of the velocity (v) changes with time, in addition to continuous change in direction, which is inherent to the circular motion owing to the requirement of the particle to follow a non-linear circular path. -
Radial acceleration

-
Tangential acceleration










