Laws of motion
1. Force
It is an agent that changes or tends to change the state of rest or of uniform motion of a body in a straight line.
Unit:N (newton)
2. Newton's Laws Of Motion
(a) Law 1: Everybody remains at rest or continues to move with uniform velocity unless an external force is applied to it.
(b) Law 2:
Gives relation between force and acceleration
i.e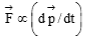
Newton’s second law : F = ma
Where F is the resultant impressed force and a is the acceleration
In, the quantity m is called “inertial mass” of body
(c) Law 3: When a body A exerts a force on another body B, B exerts an equal and opposite force on A. If one of these two forces is considered as action, then other will be reaction.
3. Commonly Used Forces
(a) Normal force: Normal to the surfaces of contact and towards the body under consideration.
(b) Weight of body: Equals to Mg and acts vertically downward.
(c) Tension in string: Along the string, away from the body under consideration.
4.Pulley Mass Systems
Unless stated otherwise, pulleys and strings are massless
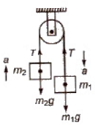
(i) When unequal masses m1 and m2 are suspended from a pulley
(m1 > m2)
m1g – T = m1a, and T – m2g = m2a
On solving equations, we get
a = ((m1 – m2) / (m1 + m2)) * g
T = 2m1m2 / (m1 + m2) * g
(ii) When a body of mass m2 is placed frictionless horizontal surface, then
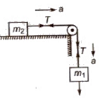
Acceleration a = m1g / (m1 + m2)
Tension in string T = m1m2g / (m1 + m2)
(iii) When a body of mass m2 is placed on a rough horizontal surface, then
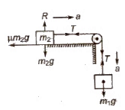
Acceleration a = ((m1 – μm2) / (m1 + m2)) * g
Tension in string T = (m1m2(1 + μ) / (m1 + m2)) * g
(iv) When two masses m1 and m2 are connected to a single mass M as shown in figure, then
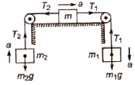
m1g – T1 = m1a …..(i)
T2 – m2g = m2a ……(ii)
T1 – T2 = Ma …….(iii)
Acceleration a = ((m1 – m2 / (m1 + m2 + M)) * g
Tension T1 = (2m2 + M / (m1 + m2 + M) * m1g
T2 = (2ma + M / (m1 + m2 + M) * m2g
(v) Motion on a smooth inclined plane, then
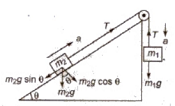
m1g – T = m1a …..(i)
T – m2g sin θ = m2a ……(ii)
Acceleration a = ((m1 – m2 sin θ/ (m1 + m2)) * g
Tension T = m1m2(1 + sin θ) g / (m1 + m2)
(vi) Motion of two bodies placed on two inclined planes having different angle of inclination, then
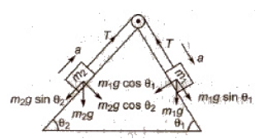
Acceleration a = (m1 sin θ1 – m2 sin θ2) g / m1 + m2
Tension T = (m1m2 / m1 + m2) * (sin θ1 – sin θ2) g
5. Stepwise Procedure to Solve Questions Based On Motion Of Connected Bodies
(a) Identify the unknown forces and accelerations.
(b) Draw FBD of bodies in the system.
(c) Resolve forces in the direction of motion and perpendicular to it.
(d) Apply F = ma in the direction of motion and a = 0 in the direction of equilibrium.
(e) Write constraint relation if required and possible.
(f) Solve the equations written in above steps to get the results.
6. Pseudo Force
In an accelerated frame of reference, Newton’s laws are not applicable unless we introduce pseudo forces.
If we are studying the motion of body of mass m, in a frame of reference with acceleration a, the pseudo force to be introduced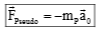 .
.
Thus for a frame of reference with angular velocity ω, the pseudo force is mω2r which is away from the centre. We say then that a centrifugal force mω2 r acts on the body, when viewed from the rotating frame.
7. Conical Pendulum
It consists of a string whose upper end is fixed and bob is tied at the other free end. The string traces the surface of the cone, the arrangement is called a conical pendulum.
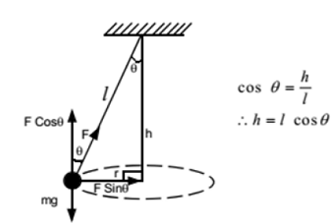
Time period of conical pendulum, 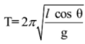
8.Apparent Weight in a Lift
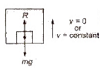
(i) When a lift is at rest or moving with a constant speed, then
R = mg
The weighing machine will read the actual weight.
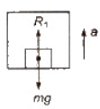
(ii) When a lift is accelerating upward, then apparent weight
R1 = m(g + a)
The weighing machine will read the apparent weight, which is more than the actual weight.
(iii) When a lift is accelerating downward, then apparent weight
R2 = m (g – a)
The weighing machine will read the apparent weight, which is less than the actual weight.
(iv) When lift is falling freely under gravity, then
R2 = m(g – g)= 0
The apparent weight of the body becomes zero.
(v) If lift is accelerating downward with an acceleration greater than g, then body will lift from floor to the ceiling of the lift.
9. Frictional Force
Frictional forces are produced due to intermolecular interactions acting between the molecules of the bodies in contact.
10. Types Of Frictional Force
(a) Static frictional force: Self adjusting force having magnitude less than or equal to μs N.
(b) Limiting frictional force: Maximum value of frictional force having value μsN. If (f)m is the maximum value of static friction, then is the coefficient of static friction. In general, = μs × normal contact force.
μs = tan θ
(c) Kinetic frictional force: If the body begins to slide on the surface, the magnitude of the frictional force rapidly decreases to a constant value fk kinetic friction.
It has value equal to μkN.
where μ k = coefficient of kinetic friction and N = normal force.
Kinetic friction is of two types:
(a) Sliding friction
(b) Rolling friction
As, rolling friction < sliding friction, therefore it is easier to roll a body than to slide.
Kinetic friction (fk) = μk R
where μk = coefficient of kinetic friction and R = normal reaction.
Angle of repose or angle of sliding It is the minimum angle of inclination of a plane with the horizontal, such that a body placed on it, just begins to slide down.
If angle of repose is a. and coefficient of limiting friction is μ, then
μs = tan α
(d) For plane inclined at an angle θ with horizontal:
If the body just slides (acceleration = 0)
μ = tan θ
If θ < tan–1 μ, the body will not slide
If θ = tan–1 μ, the body will just slide down
If θ > tan–1 μ, the body will slide with acceleration a.









