Fluids mechanics notes
Detail fluids mechanics notes
- Hooke’s law
- The force developed within a body is directly proportional to the deformation of the body within the elastic limit.
- Force constant of a spring is the force required to produce unit extension in it.
- Young’s modulus
Young’s modulus is also known as modulus of elasticity and is defined as: The mechanical property of a material to withstand the compression or the elongation with respect to its length. It is denoted as E or Y.
Young’s Modulus (also referred to as the Elastic Modulus or Tensile Modulus), is a measure of mechanical properties of linear elastic solids like rods, wires, and such. There are other numbers that give us a measure of elastic properties of a material, like Bulk modulus and shear modulus, but the value of Young’s Modulus is most commonly used. This is because it gives us information about the tensile elasticity of a material (ability to deform along an axis).
Young’s modulus describes the relationship between stress (force per unit area) and strain (proportional deformation in an object). The Young’s modulus is named after the British scientist Thomas Young. A solid object deforms when a particular load is applied to it. If the object is elastic, the body regains its original shape when the pressure is removed. Many materials are not linear and elastic beyond a small amount of deformation. The constant Young’s modulus applies only to linear elastic substances.
Young’s Modulus Formula:
Y = σ/ ε
Bulk modulus of Elasticity:
It is given by the ratio of pressure applied to the corresponding relative decrease in the volume of the material.
Mathematically, it is represented as follows:
B = ΔP/( ΔV/V)
Where:
B: Bulk modulus
ΔP: change of the pressure or force applied per unit area on the material
ΔV: change of the volume of the material due to the compression
V: Initial volume of the material in the units of in the English system and N/m2 in the metric system.
Relation Between Young's Modulus And Bulk Modulus derivation
Young's modulus is the ratio of longitudinal stress to longitudinal strain. Represented by Y and mathematically
given by:
Y = σ/ ε
On rearranging-
ε = σ/Y
When the deforming force is ling x direction-
εx = σ/Y – 1/m σ/Y – 1/m σ/Y
Here negative sign represents the reduction in diameter when longitudinal stress is along the x-axis.
1/m arise due to compression along other two direction.
When the deforming force is ling y-direction-
εy = σ/Y – 1/m σ/Y – 1/m σ/Y
When the deforming force is ling z-direction-
εz = σ/Y – 1/m σ/Y – 1/m σ/Y
The volumetric strain is given by-
εu = 3σ/Y [1 – 2/m]
The Bulk modulus is the ratio of volumetric/bulk strain to volumetric/bulk stress, represented by K and mathematically given by-
K = σ/εu
Substituting εu = 3σ/Y [1 – 2/m] in above equation we get-
K = σ/εu/y[1 – 2/m] ⇒ K = Y/3[1 – 2/m]
Hope you understood the relation and conversion between Young's modulus and the Bulk modulus of an object.
Shear Modulus of Rigidity:
Shear Modulus of elasticity is one of the measures of mechanical properties of solids. Other elastic moduli are Young's modulus and bulk modulus. The shear modulus of material gives us the ratio of shear stress to shear strain in a body.
- Measured using the Sl unit pascal or Pa.
- The dimensional formula of Shear modulus is M1L-1T-2.
- It is denoted by G
It can be used to explain how a material resists transverse deformations but this is practical for small deformations only, following which they are able to return to the original state. This is because large shearing forces lead to permanent deformations (no longer elastic body).
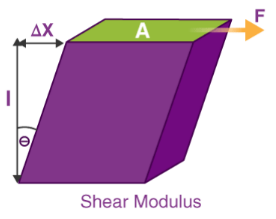
G = Txy/γzy = (F/A)/(Δx/l) = Fl/AΔx









