Properties of Determinants

Properties of Determinants

(i) A determinant formed by changing rows into columns and the columns into rows is called as transpose of a determinant and is represented by DT. The value of D = DT.

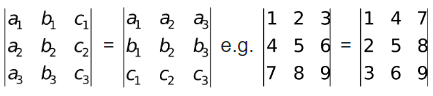
(ii) If all the elements of a row (or column) are zero, then the determinant is zero.

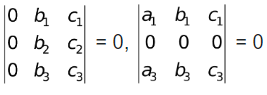
(iii) If any two rows or any two columns of a determinant are identical, then the determinant is zero.

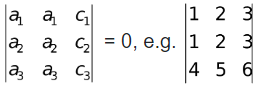 = 0, (Here 1st and IInd rows are identical)

(iv) The interchange of any two rows (columns) of the determinant results in change of it's sign.

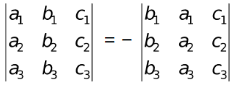 e.g.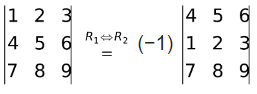

(v) If all the elements of a row (column) of a determinant are multiplied by a non-zero constant, then the determinant gets multiplied by that constant.

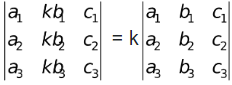  and k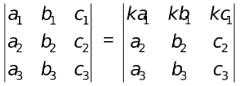

e.g. 2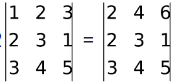

(vi) A determinant remains unaltered under a column operation of the form Ci + αCj + βCk (j, k ≠ i) or a row operation of the form Ri + αRj + βRk(j, k ≠ i).

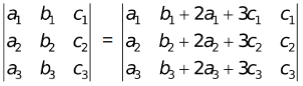
e.g.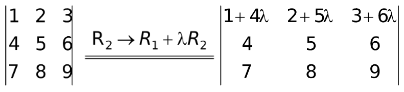

(vii) If each element of a row (column) of a determinant is a sum of two terms, then determinant can be written as sum of two determinant in following way

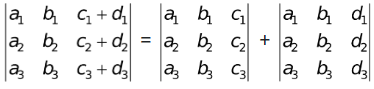
(viii) Summation of determinants

 =

And =

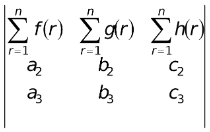
(ix) Product of two determinants

 =

=

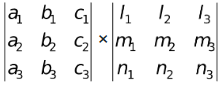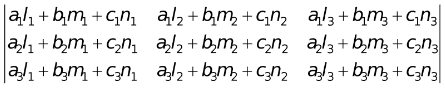
Remark:

Let Δ ≠ 0 and Δc denotes the determinant of co-factors then Δc = Δn - 1, where n ∈ N is the order of determinant Δ.