
IMPULSES OF FORCE
Force Laws of Motion of Class 9
In previous article, we leant that a moving body has momentum and that on effect (a force) is needed to stop it. It is our common experience that a smaller force takes more time to stop the body whereas a bigger force does the same in lesser time. This observation gives concept of a new quantity, force × time, which is named a impulse.
Definition :
The product of the magnitude of a force applied on a body and the time for which it is applied, is called impulse of the force. It is represented by the symbol (I).
i.e., Impulse = Force × Time
or I = F. t
The S.I. unit of impulse is Newton-second (N-s) and the C.G.S unit is dyne - second (dyne -s)
Impulse and Momentum :
From Newton’s second law of motion
Force,
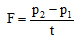 or
or
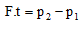
i.e., Impulse = Change in momentum
This relation is called impulse equation or momentum-impulse theorem. It has an important application in our everyday life.




