Newton's Second Law
Share
Newton's Second Law
Impluse And Momentum of Class 11
How will you catch (without braking) a raw egg moving toward you?
Obviously, you will make initial contact with the egg as far in front of your body as possible, and then move your hands backwards to bring the egg slowly to rest.
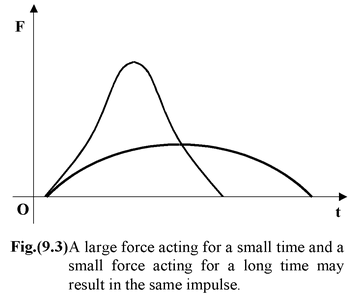
The physics of the process is simple. When the egg reaches you it has some momentum. To stop the egg you must reduce the momentum to zero by applying an impulse. That is, you must have a certain area under the F - t curve. As shown in figure (9.3), you have a choice. You can exert a large force for a short time or a small force for a long time. One way or another you must generate an area under the F - t graph equal to Δp.
The quantitative aspect of it is illustrated below.
|
From equation (9.6), we know
Using definition of Impulse, we get
For constant net force,
or If the force is not constant, then we can find the average force as
|
|
= Δ
= Δ
= 
For short intervals 
approximates the instantaneous force. In the limit as Δt approaches zero the fraction becomes the derivative.
Thus, 
= 
(9.7)
Equation (9.7) shows the momentum statement of the Newton's Second Law.
The net force acting on a particle is equal to the time rate of change of its linear momentum.
For a particle of constant mass equation (9.7) reduces to the common statement of Newton's Second Law.
= 
or = m
Example 9.5
An 150 g ball is thrown at 30 m/s. It is struck by a bat which gives it a velocity of 40 m/s in the opposite direction. If the time of contact is 10-2s, what is the average force on the ball?
Solution
If we choose the original direction as +x axis, then
= 
= m(-40 i^– 30 
)
The average force is
Fav =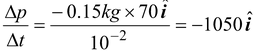 
N
Notice that this is much larger than the weight (1.5 N) of the ball.
