Rotational Kinematics
Rotational Motion of Class 11
Consider a body of arbitrary shape rotating about a fixed axis ‘O’ as shown in figure(10.2). In a given interval all the particles lying on the line OA move to their corresponding positions lying on OB.
|
Although the particles of the body have different linear displacements, they all have the same angular displacement θ, which is given by θ = s/r (10.1) The average angular velocity of the body for a finite time interval is given by
ωav = The unit of angular velocity is radian per second (rad/s). The instantaneous angular velocity is defined as
ω = |
|
|
It is the rate of change of the angular position θ with respect to time. It is a vector quantity. The direction of angular velocity is given by the right-hand rule. We hold the right hand such that when the fingers of the right hand curve in the sense of rotation, the thumb points in the direction of ω. |
|
Period and Frequency of Revolution
The period T is the time for one revolution and the frequency f is the number of revolutions per second (rev/s). The period and frequency are related as
f = 1/T (10.4)
If the angular velocity is constant, the instantaneous and average velocities are equal.
In terms period T and frequency f the angular velocity is given by
ω = 2π/T = 2πf (10.5)
The relation between linear speed and angular speed is obtained by differentiating
equation (10.1) with respect to time.
dθ/dt = 1/r ds/dt or ω = v/r
orv = ωr (10.6)
Although all particles have the same angular velocity, their speeds increase linearly with distance from the axis of rotation.
The average angular acceleration is defined as
αav =  (10.7)
(10.7)
and the instantaneous angular acceleration is defined as
α = 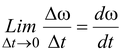 (10.8)
(10.8)
Angular acceleration is a vector quantity measured in rad/s2.
The Constant Angular Acceleration Model
When the angular acceleration is constant, we can find the change in angular velocity by integrating equation (10.8)
dω = α dt
or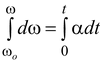 or ω - ωo = αt
or ω - ωo = αt
or 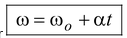 (10.9)
(10.9)
Substituting the value of ω in equation (10.3), we get
dθ = ωdt = (ωo + αt)dt
On integrating
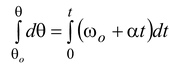
θ - θo = ωot + 1/2at2
or 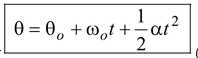 (10.10)
(10.10)
On eliminating t from equation (10.9) and (10.10), we get
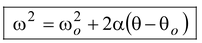 (10.11)
(10.11)
The equations (10.9), (10.10) and (10.11) are called the equations of rotation kinematics for constant angular acceleration.
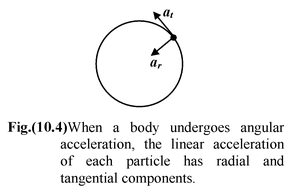
A particle moving in a circular path with speed v has a centripetal (or radial) acceleration
|
ar = If there is angular acceleration, the speed of the particle changes and thus we can find the tangential acceleration
at = The net acceleration is:
The magnitude of acceleration is given by
a = |
|
Table 10.1 Analogy Between Rotational Kinematics and Linear Kinematics
|
Quantity |
Linear |
Rotational |
|
1.Position |
x |
θ |
|
2.Displacement |
Δx |
Δθ |
|
3.Velocity |
v = dx/dt |
ω = dθ/dt |
|
4.Acceleration |
a = dv/dt |
α = dω/dt |
|
v = ∫a dt + c |
ω = ∫αdt + c |
|
|
x = ∫vdt' + c' |
θ = ∫ωdt + c' |
|
|
5. Equations of Kinematics |
v = vo + at |
ω = ωο + αt |
|
x = xo + vot + 1/2at2 |
θ = θο + ωοt + 1/2αt2 |
|
|
v2 − vo2 = 2a(x- xo) |
ω2 − ωο2 = 2α(θ − θο) |
Example 10.1
A disc starts rotating with constant angular acceleration of π rad/s2 about a fixed axis perpendicular to its plane and through its centre.
(a)Find the angular velocity of the disc after 4 s.
(b)Find the angular displacement of the disc after 4 s and
(c)Find number of turns accomplished by the disc in 4 s.
Solution
Hereα = π rad/sec2
ω0 = 0
t = 4 sec
(a)ω = 0 + (π rad/s2) × 4 sec = 4π rad/s.
(b)θ = 0 + (π rad/s2) × (16 s2) = 8 π rad.
(c)Let the number of turns be n
⇒n (2 π) rad = 8 π rad⇒n = 4
Example 10.2
A wheel rotates with an angular acceleration given by α = 4at3 - 3bt2 , where t is the time and a and b are constants. If the wheel has initial angular speed ω0, write the equations for the:
(i) angular speed
(ii) angular displacement.
Solution
(i)From equation (10.8), we know
dω = α dt
Integrating both sides, we get
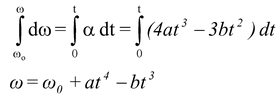
(ii)From equation (10.3), we know
dθ = ωdt
On integrating both the sides, we get
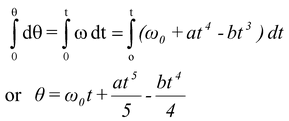
Example 10.3
A flywheel of radius 20 cm starts from rest, and has a constant angular acceleration of 60 rad/s2. Find
(a)the magnitude of the net linear acceleration of a point on the rim after 0.15 s
(b) the number of revolutions completed in 0.25 s
Solution
(a)The tangential acceleration is constant and given by
at = αr = (60 rad/s2)(0.2 m) = 12 m/s2
In order to calculate the radial acceleration we first need to find the angular velocity at the given time. From equation (10.9), we have
ω = ωo + αt = 0 + (60 rad/s2)(0.15 s) = 9 rad/s
Then using equation (10.12), we have
ar = ω2r = (81 rad2/s2)(0.2 m) = 16.2 m/s2
The magnitude of the net linear acceleration is
a = 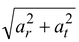 = 20.2 m/s2
= 20.2 m/s2
(b)From equation (10.10),
0 = 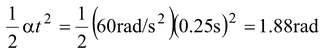
This corresponds to (1.88 rad) (1 rev/2π rad) = 0.3 rev
 (10.2)
(10.2)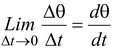 (10.3)
(10.3)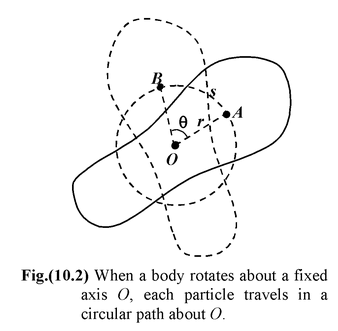

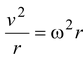 (10.12)
(10.12)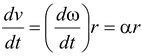 (10.13)
(10.13)