Rotational Work and Energy
Rotational Motion of Class 11
The rotational work done by a force about the fixed axis of rotation is defined as
Wrot = 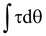 (10.23)
(10.23)
Where τ is the torque produced by the force, and dθ is the infinitesimally small angular displacement about the axis.
The rotational kinetic energy of a body about a fixed rotational axis is defined as
Krot = 1/2 Iω2 (10.24)
where I is the moment of inertia about the axis.
Work – Energy Theorem
In complete analog to the work energy theorem for the translatory motion, it can be stated for rotational motion as:
Wrot = ΔKrot (10.25)
The net rotational work done by the forces is equal to the change in rotational kinetic energy of the body.
Conservation of Mechanical Energy
In the absence of dissipative work done by non-conservative forces, the total mechanical energy of a system is conserved.
ΔK + ΔU = 0
or Kf + Uf = Ki + Ui (10.26)
Example 10.12
|
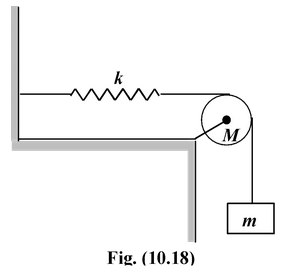
A block of mass m = 4 kg is attached to a spring (k = 32 N/m) by a rope that hangs over a pulley of mass M = 8 kg. If the system starts from rest with the spring unextended, find the speed of the block after it falls 1m. Treat the pulley as a disc, so I = 1/2MR2 Solution Since the rim of the pulley moves at the same speed as the block, the speed of the block and the angular velocity of the pulley related by v = ωR. |
|
When the block falls by a distance x, its potential energy decreases (ΔUg = -mgx); the potential energy of the spring increases (ΔUs = +1/2kx2), and both the block and the pulley gain kinetic energy (ΔK = 1/2mv2 + 1/2Iω2).
From the conservation of mechanical energy, ΔK + ΔU = 0,
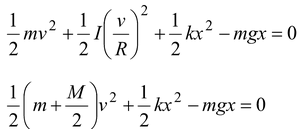
Note that R was not needed.
Putting m = 4 kg; M = 8 kg; k = 32 N/m; x = 1m

4v2 + 16 – 40 = 0
orv = 2.4 m/s
Rotational Power
In complete analog with the linear motion, the instantaneous rotational power is defined as
Prot =  (10.27)
(10.27)
|
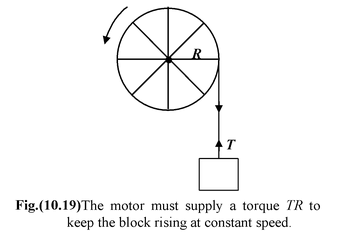
Example 10.13 A motor rotates a pulley of radius 25 cm at 20 rpm. A rope around the pulley lifts a 50 kg block, as shown in figure. What is the power output of the motor? Solution The tension in the rope is equal to the weight since there is no acceleration. Thus, T = 500 N. |
|
Therefore, τ = TR = (500)(0.25) = 125 Nm.
Angular velocity, ω = 2πN/60
or ω = 2π(20)/60 = 2π/3 rad/s
The power required is
P = τω = (125 N m) = 2π/3 rad/s = 260 W