Electromagnetic Induction
Electromagnetic induction class 12 notes
Induced Emf
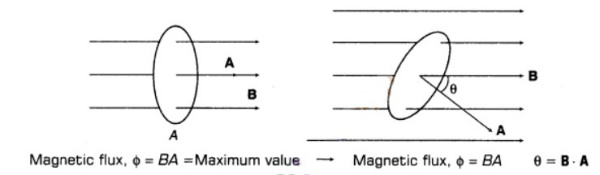
Magnetic Flux : The magnetic flux linked with any surface is equal to total number of magnetic lines of force passing normally through it. It is a scalar quantity.
Suppose, we consider small area dA in field B, then φ = ∫ B. dA
SI Unit of magnetic flux is Weber (Wb).
CGS Unit of magnetic flux is Maxwell (Mx).
1 Wb = 108 Mx = 1 Tm2
Magnetic Flux is a scalar quantity and its dimensional formula is [ML2T-2A-1]
The phenomenon of generation of current or emf by changing the magnetic flux is known as Electromagnetic Induction EMI).
Faraday’s Law of Electromagnetic Induction
First Law : Whenever magnetic flux linked with the closed loop or circuit changes, an emf induces in the loop or circuit which lasts so long as change in flux continuous.
Second Law : The induced emf in a closed loop or circuit is directly proportional to the rate of change of magnetic flux linked with the closed loop or circuit
e ∝ (-)ΔΦ/Δt ⇒ e = -N(ΔΦ/Δt)
where, N = number of turns in loop.
Negative sign indicates the Lenz’s law.
Lenz’s Law : The direction of induced emf or induced current is such that it always opposes the cause that produce it.
If N is the number of turns and R is the resistance of a coil. The magnetic flux linked with its each turn changes by dФ in short time interval dt, then induced current flowing through the coil is
I = |e|/R = 1/R N(ΔΦ/Δt)
6. If induced current is produced in a coil rotated in a uniform magnetic field, then
I = NBA ω sinωt/R = I0 sinωt
where, I0 = NBA ω/R = Peak value of induced current
Motional emf : The potential difference induced in a conductor of length l moving with velocity v, in a direction perpendicular to magnetic field B is given by
ε = ∫ (v x B) dl = vBl
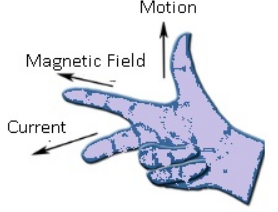
Fleming’s Right Hand Rule: If the thumb, forefinger and middle finger of right hand are stretched mutually perpendicular to each other such that the forefinger points the direction of magnetic field, thumb points towards the direction of magnetic force, then middle finger points towards the direction of induced current in the conductor.
The induced emf: developed between two ends of conductor of length l rotating about one end with angular velocity ω in a direction perpendicular to magnetic field is given by,
ε = Bωl2/2
The induced emf can be produced in a coil by
- putting the coil/loop/circuit in varying magnetic field.
- changing the area A of the coil inside the magnetic field,
- changing the angle 0 between B and A.