Electrostatics
Coulomb’s Law of Electrostatics
Electrostatic force of interaction acting between two stationary charges is given by
F = 1 / 4π εo q1q2 / r2
where q1, q2 are magnitude of point charges, r is the distance between them and εo is permittivity of free space.
Here, 1 / 4πεo = (10-7 N – s2 / C2)C2
Substituting value of c = 2.99792458 X 108 m/s, We get 1 / 4πεo = 8.99 x 109N-m2/C2 In examples and problems we will often use the approximate value,
1 / 4πεo = 9 * 109N-m2/C2 The value of εo is 8.85 * 10-12 C2 / N-mC2. If there is another medium between the point charges except air or vacuum, then εo is replaced by εoK or εoεr or ε.
where K or εr is called dielectric constant or relative permittivity of the medium. K = εr = ε / εo where, ε = permittivity of the medium.
For air or vacuum, K = 1 For water, K = 81 For metals, K = ∞
Coulomb’s Law in Vector Form
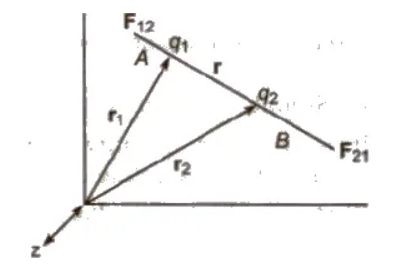
Force on q2 due to q1,
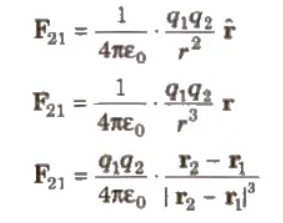
The above equations give the Coulomb’s law in vector form.
Force on q1 due to q2 = – Force on q2 due to q1
F12 = – F21 F12 = q1q2 / 4πε . r1 – r2 / |r1 – r2|3
The forces due to two point charges are parallel to the line joining point charges; such forces are called central forces and electrostatic forces are conservative forces.
Electric Field
The space in the surrounding of any charge in which its influence can be experienced by other charges is called electric field.
Electric Field Lines
An electric field line is an imaginary line or curve drawn through a region of space so that its tangent at any point is in the direction of the electric field vector at that point. The relative closeness of the lines at some place give an idea about the intensity of electric field at that point.”
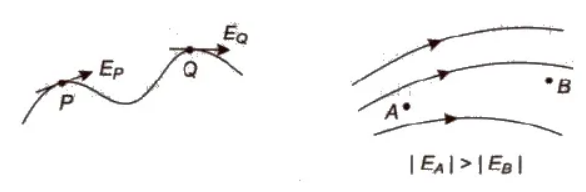
Two lines can never intersect.
Electric field lines always begin on a positive charge and end on a negative charge and do not start or stop in mid space.
Electric Field Intensity (E)
The electrostatic force acting per unit positive charge on a point in electric field is called electric field intensity at that point.
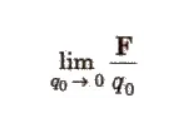
Electric field intensity E = Its SI unit is NC-1 or Vim and its dimension is [MLT-3 A-1]. It is a vector quantity and its direction is in the direction of electrostatic force acting on positive charge. Electric field intensity due to a point charge q at a distance r is given by E = 1 / 4π εo q / r2
Electric Potential (V)
Electric potential at any point is equal to the work done per positive charge in carrying it from infinity to that point in electric field. Electric potential, V = W / q Its SI unit is J / C or volt and its dimension is [ML2T-3A-1]. It is a scalar quantity. Electric potential due to a point charge at a distance r is given by v = 1 / 4π εo q / r
Potential Gradient
The rate of change of potential with distance in electric field is called potential gradient.
Potential gradient = dV / dr
Its unit is V / m.
Relation between potential gradient and electric field intensity is given by
E = – (dV / dr)
Equipotential surface is an imaginary surface joining the points of same potential in an electric field. So, we can say that the potential difference between any two points on an equipotential surface is zero. The electric lines of force at each point of an equipotential surface are normal to the surface.
Electric Lines of Force
Electric Flux (φE)
Electric flux over an area is equal to the total number of electric field lines crossing this area. Electric flux through a small area element dS is given by
φE = E. dS
where E= electric field intensity and dS = area vector.
Its SI unit is N – m2C-1.
Gauss’s Theorem
The electric flux over any closed surface is 1 / εo times the total charge enclosed by that surface, i.e.,
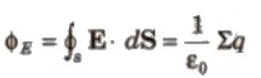
CBSE Class 11 Physics Notes Electrostatics
If a charge q is placed at the centre of a cube, then
total electric flux linked with the whole cube = q / εo
electric flux linked with one face of the cube = q / 6 εo
(i) Electric Field at Any Point on the Axis of a Uniformly Charged Ring A ring-shaped conductor with radius a carries total charge Q uniformly distributed around it. Let us calculate the electric field at a point P that lies on the axis of the ring at distance x from its centre.
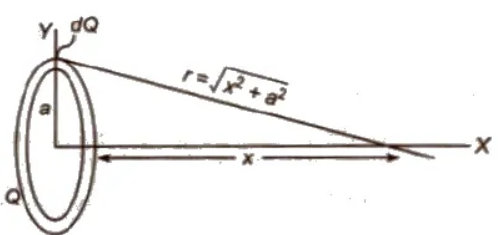
Ex = 1 / 4π εo * xQ / (x2 + a2)3/2
The maximum value of electric field
Ex = 1 / 4π εo (2Q / 3√3R2)
Electric Potential due to a Charged Conducting Spherical Shell
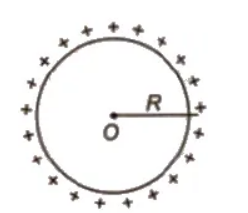
(a) At an extreme point (r > R)
V = 1 / 4π εo q / r
(b) At the surface of a shell (r = R)
V = 1 / 4π εo q / R
(c) At an internal point (r < R)
V = 1 / 4π εo q / R
Therefore potential inside a charged conducting spherical shell equal to the potential at its surface.
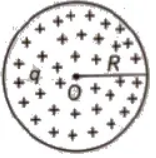
(iv) Electric Field and Potential due to a Charged Non-Conducting Sphere

(v) Electric Field Intensity due to an Infinite Line Charge
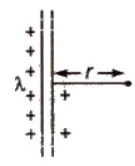
E = 1 / 2 π εo λ / r
where λ is linear charge density and r is distance from the line charge.
(vi) Electric Field Near an Infinite Plane Sheet of Charge
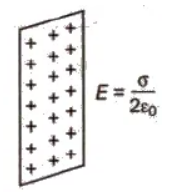
E = σ / 2 εo
where σ = surface charge density.
If infinite plane sheet has uniform thickness, then
E = σ / εo
If infinite plane sheet has uniform thickness, then
An electric dipole consists of two equal and opposite point charges separated by a very small distance. e.g., a molecule of HCL, a molecule of water etc.
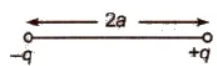
- Electric Dipole Moment p = q * 2 l
- Its SI unit is ‘coulomb-metre’ and its dimension is [LTA).
- It is a vector quantity and its direction is from negative charge towards positive charge.
Electric Field Intensity and Potential due to an Electric Dipole
(i) On Axial Line
- Electric field intensity E = 1 / 4 π εo * 2 pr / (r2 – a2)2
- If r > > 2a, then E = 1 / 4 π εo * 2 p / r3
- Electric potential V = 1 / 4 π εo * p / (r2 – a2)
-
- I fr > > 2a, then V = 1 / 4 π εo * p / r2
(ii) On Equatorial Line
- Electric field intensity E = 1 / 4 π εo * p / (r2 + a2)3 / 2
-
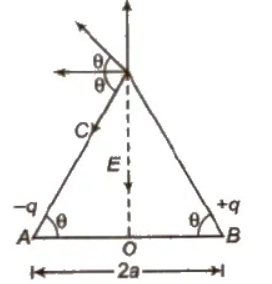
- If r > > 2a, then E = 1 / 4 π εo * p / r3
- Electric potential V = 0
(iii) At any Point along a Line Making θ Angle with Axis
- Electric field intensity E = 1 / 4 π εo * p √1 + 3 cos2 θ / r3
-
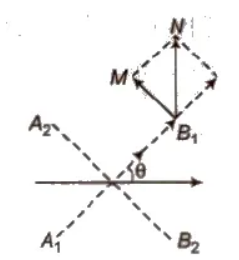
- Electric potential V = 1 / 4 π εo * p cos θ / (r2 – a2 cos2 θ)
- If r > > 2a, then V = 1 / 4 π εo * p cos θ / r2
Torque
- Torque acting on an electric dipole placed in uniform electric field is given by
- τ = Ep sin θ or τ = p * E
- When θ = 90°, then ‘τmax = Ep
When electric dipole is parallel to electric field, it is in stable equilibrium and when it is anti-parallel to electric field, it is in unstable equilibrium.
Work Done
- Work done is rotating an electric dipole in a uniform electric field from angle θ1 to θ2 is given by
- W = Ep (cos θ1 – cos θ2)
- If initially it is in the direction of electric field, then work done in rotating through an angle θ, W = Ep (1 – cos θ).
Potential Energy
Potential energy of an electric dipole in a uniform electric field is given by U = – pE cos θ.
Dipole in Non-uniform Electric Field
- When an electric dipole is placed in a non-uniform electric field, then a resultant force as well as a torque act on it.
- Net force on electric dipole = (qE1 – qE2), along the direction of greater e ecmc field intensity.
- Therefore electric dipole undergo rotational as well as linear motion.
Potential Energy of Charge System
Two point charge system, contains charges q1 and q2 separated by a distance r is given by U = 1 / 4 π εo * q1q2 / r
Three point charge system
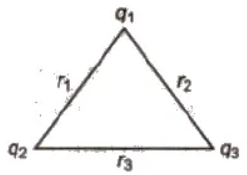
U = 1 / 4 π εo * [q12 / r1 + q2q3 / r2 + q3q2 / r3
Important Points
- When charge is given to a soap bubble its size gets increased.
- In equilibrium for a charged soap bubble, pressure due to surface tension
- = electric pressure due to charging
- 4T / r = σ2 / 2 εo
- or 4T / r = 1 / 2 εo (q / 4 πr2)2
- or q = 8 πr √2 εo rT
- where, r is radius of soap bubble and T is surface tension of soap bubble.
Behaviour of a Conductor in an Electrostatic Field
- Electric field at any point inside the conductor is zero.
- Electric field at any point on the surface of charged conductor is directly proportional to the surface density of charge at that point, but electric potential does not depend upon the surface density of charge.
- Electric potential at any point inside the conductor is constant and equal to potential.
Electrostatic Shielding
- The process of protecting certain field from external electric field is called, electrostatic shielding.
- Electrostatic shielding is achieved by enclosing that region in a closed metallic chamber.
Dielectric
Dielectrics are of two types Non-polar Dielectric The non-polar dielectrics (like N2, O2, benzene, methane) etc. are made up of non-polar atoms/molecules, in which the centre of positive charge coincides with the centre of negative charge of the atom/molecule.
Polar Dielectric
The polar dielectric (like H2O, CO2, NH3 etc) are made up of polar atoms/molecules, in which the centre of positive charge does not coincide with the centre of negative charge of the atom.
Capacitor
- A capacitor is a device which is used to store huge charge over it, without changing its dimensions.
- When an earthed conductor is placed near a charged conductor, then it decreases its potential and therefore more charge can be stored over it.
- A capacitor is a pair of two conductors of any shape, close to each other and have equal and opposite charges.
- Capacitance of a conductor C = q / V
- Its 81 unit is coulomb/volt or farad.
- Its other units are 1 μ F = 10-6 F
- 1 μμ F = 1 pF = 10-12 F
- Its dimensional formula is [M-1L-2T4A2].
Capacitance of an Isolated Spherical Conductor
- C = 4 π εo K R
-
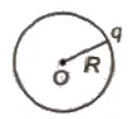
- For air K = 1
- ∴ C = 4 π εo R = R / 9 * 109
Parallel Plate Capacitor
- The capacitor with two plates arranges in parallel is shown below.
-
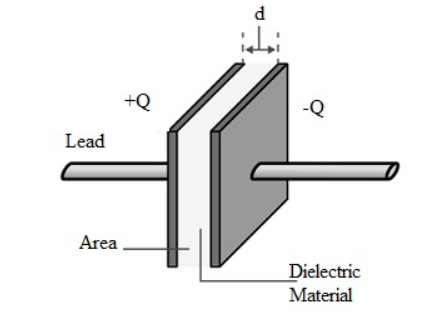
- The first plate in the capacitor carries ‘+Q’ charge and the second plate carries ‘–Q’ charge. The area between these plates can be denoted with ‘A’ and the distance(d). Here, ‘d’ is smaller than the area of the plates (d < < A). When the whole charge on the first plate is ‘Q’ & ‘A’ is the area of the plate, then the density of surface charge can be derived as
- σ =Q/A
- Similarly, when the whole charge on the second plate is ‘-Q’ & is the area of the plate is ‘A’, then the density of surface charge can be derived as
- σ = -Q/A
- The regions of this capacitor can be divided into three divisions like area1, area2, and area3. Area 1 is left to the plate1, area 2 is between the planes & area 3 is the right of the second plate. The electric field can be calculated in the region around the capacitor. Here, the electric field is consistent & its path is from the +Ve plate to the –Ve plate.
- V = Exd = 1/ε(Qd/A)
- The capacitance of the parallel plate can be derived as C = Q/V = εoA/d
- The capacitance of a parallel plate capacitor with 2 dielectrics is shown below. Each plate area is Am2 and separated with d-meter distance. The two dielectrics are K1 & k2, then the capacitance will be like the following.
- The capacitance of primary half of the capacitor width is d/2 = C1=> K1Aϵ0/ d/2=> 2K1Aϵ0/d
- Similarly, the capacitance of the next half of the capacitor is C2 = 2K2Aϵ0/d
- Once these two capacitors are connected in series then the net capacitance will be
- Ceff= C1C2/C1+C2= 2Aϵ0/d( K1K2/ /K1+K2)
Capacitors in series and parallel combinations
For practical applications , two or more capacitors are often used in combination and their total capacitance C must be known.To find total capacitance of the arrangement of capacitor we would use equation
Q=CV
(i) Parallel combination of capacitors
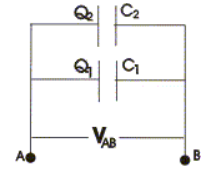
- Parallel combination of capacitorsA. Similarly left hand side plates of capacitors would also be at same common potential VB.
- Thus in this case potential difference VAB=VA-VB would be same for both the capacitors, and charges
- Q1 and Q2 on both the capacitors are not necessarily equal. So,
- Q1=C1V and Q2=C2V
- Thus charge stored is divided amongst both the capacitors in direct proportion to their capacitance. Total charge on both the capacitors is,
-
Total charge on both the capacitors is,
Q=Q1+Q2
=V(C1+C2) and
Q/V=C1+C2 - So system is equivalent to a single capacitor of capacitance
- C=Q/V
where,
When capacitors are connected in parallel their resultant capacitance C is the sum of their individual capacitances.
The value of equivalent capacitance of system is greater then the greatest individual one. If there are number of capacitors connected in parallel then their equivalent capacitance would be
C=C1+C2+ C3...........
Series combination of capacitors
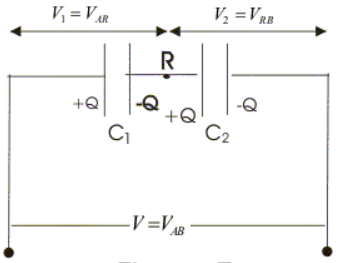
- Both the points A and B are maintained at constant potential difference VAB.
- In series combination of capacitors right hand plate of first capacitor is connected to left hand plate of next capacitor and combination may be extended foe any number of capacitors.
- In series combination of capacitors all the capacitors would have same charge.
- Now potential difference across individual capacitors are given by
VAR=Q/C1
and,
VRB=Q/C2
Sum of VAR and VRB would be equal to applied potential difference V so,
V=VAB=VAR+VRB
=Q(1/C1 + 1/C2)
or,
where
i.e., resultant capacitance of series combination C=Q/V, is the ratio of charge to total potential difference across the two capacitors connected in series.
So, from equation 12 we say that to find resultant capacitance of capacitors connected in series, we need to add reciprocals of their individual capacitances and C is always less then the smallest individual capacitance.
Result in equation 12 can be summarized for any number of capacitors i.e.,









