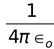Bohr's Model Of An Atom

Neil Bohr proposed the Bohr atomic model in 1915. It came about through the transformation of Rutherford's atomic model. Rutherford's model introduces the nuclear atom model, explaining that negative charge electrons surround the nucleus (positively charged).

Postulates of Bohr’s Atomic Model

• Electrons revolve around the nucleus in specified circular paths called orbits or shells.
• Each orbit or shell is associated with a definite amount of energy. Hence these are also called energy levels and are designated K, L, M, N respectively.
• The energy associated with a certain energy level increases with the increase of its distance from the nucleus. Hence if the energy associated with the K, L, M, N shells are E₁,E₂,E₃............ respectively, then E₁<E₂<E₃................etc.
• As long as the electron revolves in a particular orbit, the electron does not lose its energy. Therefore, these orbits are called stationary orbits and the electrons are said to be in stationary energy states.
• An electron jumps from a lower energy level to a higher energy level, by absorbing energy, but when it jump from a higher to lower energy level, the energy is emitted in the form of electromagnetic radiation.

Limitations of Bohr’s Model of an Atom

• Bohr's atomic model failed to explain the Zeeman Effect (effect of a magnetic field on the atomic spectra).
• It also failed to explain the effect of Stark (the effect of electric field on the atomic spectra).
• Violates Heisenberg's Uncertainty Policy.
• It could not define spectra obtained from large atoms.

Radius and Energy levels of Hydrogen Atom

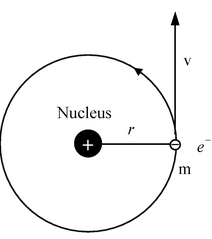
Consider an electron of mass ‘m’ and charge ‘e’ revolving around a nucleus of charge Ze (where, Z= atomic number and e is the charge of a proton) with a velocity v and r is the radius of the orbit in which the electron is revolving.

For an electron orbiting in a hydrogen atom the necessary centripetal force is the electrostatic force of attraction between the negative electron and the massive, positively charged proton that is the nucleus.

Since the electrostatic force balances the centrifugal force, for the stable electron orbit. i.e., electrostatic force = centrifugal force. Thus,

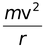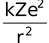∴ = …(1)

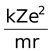or v2 = …(2)

According to Bohr’s postulate of angular momentum quantization, we have

or mvr =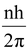

or v =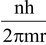

or v2 = 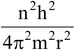…(3)

Equating equation (2) and (3) we get

=

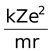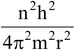
∴r =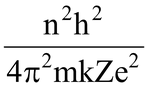

where n = 1,2,3 - - - - - ∞

The greater the value of n, farther is the energy level from the nucleus, and greater is the radius of the orbit.

The radius of the smallest orbit (n=1) for hydrogen atom (Z=1).

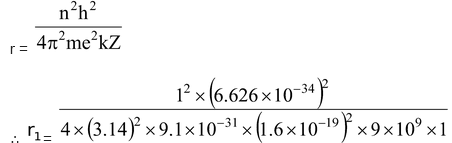
= 5.29 ×10^-11 m = 0.529 Å

Radius of nth orbit for an atom with atomic number Z is simply written as

rn = 0.529 × n²/ZÅ

Calculation of Velocity of an Electron

Velocity of electron, v = 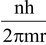…(4)

Radius of the nth orbit, r =.

Substituting value of r in equation (4)

Velocity of the electron in the nth orbit is given as

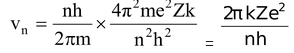
Velocity of electron in the first orbit of hydrogen atom is

v1 = 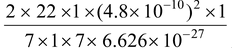= 2.18 ×10⁸ cm/s

∴ velocity of an electron in the nth orbit of an atom is given as

vn = 2.18 ×10⁸ xZ/n cm/s

Calculation of energy of an electron

The total energy E of an electron is the sum of kinetic energy and potential energy.

Kinetic energy of an electron = 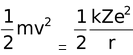  [Putting the value from equation (1)]

Potential energy =

The −ve sign of the potential energy of the electron is due to the fact that electron is attracted towards the nucleus and energy is released (at infinity the potential energy of the electron is zero).

Total energy,

E = K.E. + P. E.

where n = 1,2,3……….∞

This expression shows that only certain energies are allowed to the electron.

Since this energy expression consist of so many fundamental constant, we are giving you the following simplified expressions.

E = –21.8 ×10^-12×Z²/n² erg per atom

= –21.8 ×10^-19×Z²/n²J per atom

= –13.6 × Z²/n² eV per atom

1 electron volt is defined as the amount of energy gained by an electron when it accelerates through a field of 1V.

∴ 1 eV = 1.6 ×10^-19 J

1eV = 3.83 ×10^-23kcal

1eV = 1.602 ×10^-12erg

E = –313.6 ×Z²/n² kcal / mole (1 cal = 4.18 J)

If any students need to take the online test to check their concepts or undertstanding then they can visit Online Test Atomic Structure.

Also Check

1. Model's of Atom
2. Dalton's Atomic Theory