Quantum Numbers And Atomic Orbitals

Bohrs modal unable to describe the entire model of an Atom there for with the help of Schrodinger wave equation orbital concept introduce, according to this electron are present in orbitals. The detail theory of orbital concept can be learned by the help of quantum number.

Each electron in an atom is described by four different quantum numbers, three of which (n, λ, m) specify the wave function that gives the probability of finding the electron at various points in space. A wave function for an electron in an atom is called an atomic orbital. An atomic orbital is pictured qualitatively by describing the region of space where the probability of finding the electrons is maximum.

Quantum numbers may be defined as a set of four numbers with the help of which we can get complete information about all the electrons in an atom i.e. location, energy, the type of orbital occupied, shape and orientation of that orbital etc.

Principal Quantum Number (n)

It tells us about the shell in which the electron resides and is denoted by the letter 'n'. It can have any positive value 1, 2, 3 and so on. It gives the following information:

• It gives the average distance of the electron from the nucleus.
• It determines the energy of the electron in hydrogen atom and hydrogen like species.
•  The maximum number of electron present in any principal shell is given by 2n2 where n is the number of principal shell.

Shell KLMN

Principal quantum number (n)1234

Maximum number of electrons281832

Azimuthal or Angular Momentum Quantum Number (λ)

This represents the number of subshells present in the main shell and is denoted by λ. It can have any integral value ranging from 0 to n−1. This quantum number gives the following information:

(i) The number of subshells present in the main shell.

(ii) The shape of the subshells.

Magnetic Quantum Number (m)

An electron due to its angular motion around the nucleus generates an electric field. This electric field is expected to produce a magnetic field. Under the influence of external magnetic field, the electrons of a subshell can orient themselves in certain preferred regions of space around the nucleus called orbitals. The magnetic quantum number determines the number of preferred orientations of the electron present in a subshell. The number of allowed orientations depend on the value of azimuthal quantum number (λ. Magnetic quantum number (m) can assume all integral values between –λ to +λ including zero. Thus m can be +1, 0, −1 for λ = 1 and for λ = 2, m will have five values i.e., +2, +1, 0, −1, −2.

Spin Quantum Number (s)

Just like earth which not only revolves around the sun but also spins about its own axis, an electron in an atom not only revolves around the nucleus but also spins about its own axis. Since an electron can spin either in clockwise direction or in anticlockwise direction, therefore for any particular value of magnetic quantum number, spin quantum number can have two values i.e. +1/2 and –1/2 and these are represented by two arrows pointing in the opposite directions i.e. and 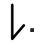. When an electron goes to a vacant orbital, it can have a clockwise or anticlockwise spin i.e. +1/2 or –1/2.

This quantum number helps us to explain the magnetic properties of the substances.

Table: Permissible Values of Quantum Numbers for Atomic Orbitals

Shapes of Orbitals

An orbital is the region of space around the nucleus within which the probability of finding an electron of a given energy is maximum (90–95%). The shape of this region (electron cloud) gives the shape of the orbital. It is basically determined by the azimuthal quantum number (λ), while the orientation of orbital depends on the magnetic quantum number (m).

Let us now see the shapes of orbitals in the various subshells.

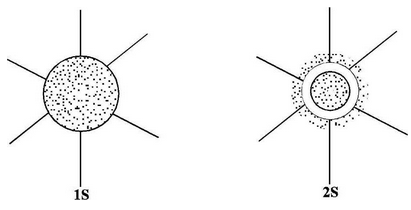
s–orbitals (λ = 0)

These orbitals are spherical and symmetrical about the nucleus. The probability of finding the electron is zero near the nucleus and keeps on increasing as the distance from the nucleus increases, becomes maximum and thereafter decreases. There is vacant space between two successive s–orbitals known as radial node or nodal surface. But there is no radial node for 1s orbital since it is starting from the nucleus.

The size of the orbital depends upon the value of principal quantum number(n). Greater the value of n, larger is the size of the orbital. Therefore, 2s orbital is larger than 1s orbital but both of them are non-directional and spherically symmetrical in shape.

p–orbitals (λ=1)

The probability of finding the p–electron is maximum in two lobes on the opposite sides of the nucleus. This gives rise to a dumb–bell shape for the p–orbital. For p–orbital λ = 1. Hence m = –1, 0, +1. Thus, p–orbital have three different orientations. These are designated as px, py&pz depending upon whether the density of electron is maximum along the x, y and z axis, respectively. They are symmetrical but have directional characters. The two lobes of p–orbitals are separated by a nodal plane, where the probability of finding electron is zero.

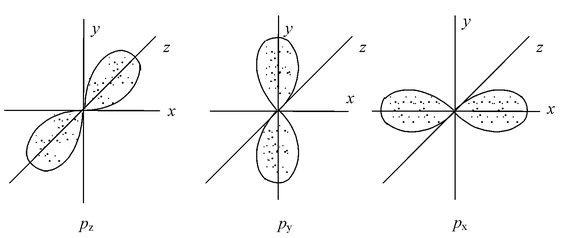
The three p orbitals belonging to a particular energy shell have equal energies and are called degenerate orbitals.

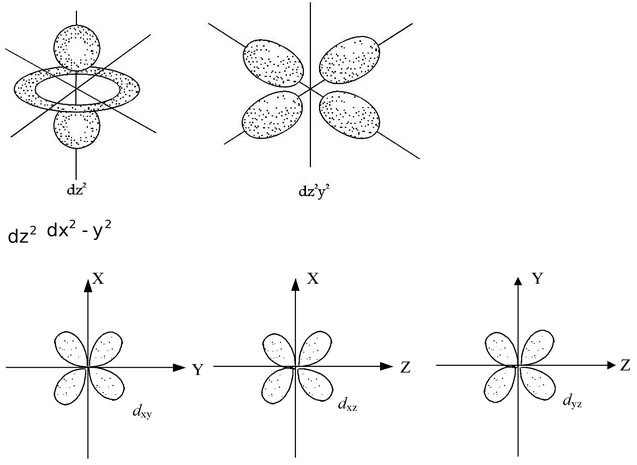
d–orbitals (λ =2)

For d–orbitals, λ=2. Hence m = –2, –1, 0, +1, +2. Thus there are 5 d−orbitals. They have relatively complex geometry. Out of the five orbitals, the three (dxy, dyz,dzx) project in between the axis and the other two 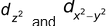lie along the axis.