Kohlrausch’s Law Of Independent Migration Of Ions

Kohlrausch’s Law Of Independent Migration Of Ions

While investigating the equivalent conductances at infinite dilution (λo), Kohlrausch found that when salts of potassium and sodium with a common anion are taken, the difference in their λo−values was found to be same irrespective of the nature of the anion. That is etc. Similar results were also obtained with other pairs of salts having either a common anion or a common cation. A few of the results are shown below.

Table: λo−Values for pairs of electrolytes (25°C)

Such constancy in the difference of λo−values of two salts having a common ion is possible only if each ion makes a definite contribution towards the conductivity of the solution irrespective of the value of the other ion. Thus,

Hence, whatever salts of sodium and potassium be taken, provided the salts are taken at infinite dilution with common anion the difference in λo value will be always same.

Kohlrausch therefore proposed that at infinite dilution, each ion makes a definite contribution towards the equivalent conductance of the electrolyte. This contribution is independent of the other ion with which it is present in the solution. The value of the equivalent conductance at infinite dilution (λo) of an electrolyte is the sum of contributions of the two ions, such that

λo = …(iv)

where and are the contributions of the cation and anion respectively, called ‘ion conductances’.

That is, at infinite dilution, the equivalent conductance is the sum of ion conductances, which are characteristic of each ion species. This is commonly known a the law of independent migration of ions.

The individual ionic conductances are usually determined from their transport number at infinite dilutions. At infinite dilution, an electrolyte is completely dissociated and there is no interionic attraction. In conveying a current, the conduction due to the cations would depend upon their charge and their speed. In other words, ion conductance lc will depend upon charge (n+ z+ e) carried to the cathode and the speed u.

or = k₁n+ z+ eu

= k u

Similarly for the anions, = k₁n− z− ev

∴ From equation, (iv)

λo = + = k₁n+ z+ eu + k₁n− z− ev

Now, the net charges released at the cathode and anode being equal

∴ k₁z+ n+ e = k₁ z− n− e

∴ λo = k (u + v)

where k = k₁ z+ n+ e

= k₁ z− n− e

∴

Hence from equation, (v) i.e. and

The zero−subscripts are used to indicate the state of infinite dilution in the application of these relations.

The transport numbers measured at low concentrations of an electrolyte are extrapolated to zero concentration to obtain and . The knowledge of the transport numbers (to) together with a determination of λo would enable us to obtain the values of ion conductances (lo).

(Application: In the case of weak electrolytes λo, the conductance at infinite dilution cannot be directly obtained. In fact, the law of independent migration of ions is used for finding out λo for weak electrolytes. To illustrate: λo for acetic acid is evaluated by determining the equivalent conductance of three strong electrolytes separately, namely, HCl, NaCl and NaAc. It is easily seen.

Since the quantities on the left−hand side are experimentally determined, λo is known. This method is employed for other weak electrolytes also).

Example 6

By how much is the oxidising power of the couple decreases if the H+ concentration is decreased from 1 M to 10⁻⁴ M at 25°C. Assume other species have no change in concentration.

Solution

In acidic medium, acts as oxidising agent as per the reaction

+ 8H+ + 5e− Mn²⁺ + 4H₂O

∴ (E₁ − E₂) = = 0.3776 V

Thus, the oxidising power of couple decreases by 0.3776 V from its standard value.

Example 7

EMF of the following cell is 0.67 V at 298 K.

Pt | H₂ (1 atm) | H+ (pH = X) || KCl (1 N) | Hg₂Cl₂(s) | Hg

Calculate the pH of anode compartment. Given = 0.28 V

Solution

At anode: H₂ 2H⁺ + 2e−

At cathode: Hg₂Cl₂ + 2e− 2Hg + 2Cl−

⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯

Net reaction: H₂ + Hg₂Cl₂ 2H+ + 2Hg + 2Cl−

∴Ecell = −−

0.67 = 0.28 − = 0.28 − 0.059 log [H+]

0.67 = 0.28 + 0.059 pH

∴pH = 6.61

Example 8

The standard reduction potential of the Ag+ | Ag electrode at 298 K is 0.799 V. K</spansp of AgI is 8.7 × 10⁻¹⁷. Evaluate the potential of the Ag+ | Ag electrode in a saturated solution of AgI. Also calculate the standard reduction potential of I− | AgI | Ag electrode.

Solution

Ag+ + e− Ag

= 0.799 − 0.059 log = 0.325 V

AgI Ag+ + I− …(i)

Ag+ + e− Ag …(ii)

⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯

AgI + e− Ag + I− …(iii)

We have learnt that metal−insoluble salt−anion electrode and metal−metal ion electrode has same potentials. Thus, equation (ii) and (iii) would have same reduction potential.

∴

∴ 0.325 = − 0.059 log = − 0.059 log

∴ = −0.149 V

Example 9

Calculate the EMF of the electrode-concentration cell

Zn–Hg(c1) | Zn²⁺(aq) | Zn–Hg(c2)

at 25 °C, if the concentrations of the zinc amalgam are: c</span1 = 2 g per 100 g of mercury and c</span2 = 1 g per 100 g of mercury.

Solution

The cell reactions in this case are

At cathode: Zn²⁺ + 2e– Zn(c2) (Reduction)

At anode: Zn(c1) Zn²⁺ + 2e– (Oxidation)

Net reaction: Zn(c1) Zn(c2)

∴ = 8.8 × 10^–3 V

Example 10

Calculate the EMF of the concentration cell consisting of zinc electrodes, one immersed in a solution of 0.01 M Zn²⁺ ions and the other in a solution of 0.1 M Zn²⁺ ions at 25 °C. The two solutions are separated by a salt bridge.

Solution

The cell may be represented as

Zn | Zn²⁺ (0.01 M)⏐⏐Zn²⁺ (0.1 M) | Zn

The EMF of the cell is given by

= = 0.0295 V

Example 11

Calculate emf of the cell

Pt | H₂ | CH₃COOH (0.1 M) || NH₄OH (0.01 M) | H₂ | Pt

Ka for CH₃COOH = 1.8 × 10⁻⁵ and Kb for NH₄OH = 1.8 × 10⁻⁵

Solution

For CH₃COOH

CH₃COOH CH₃COO + H+

∴ Ka =

or Ka = or [H+] =

∴ [H+] = 1.3461 × 10³ M

For NH₄OH

NH₄OH + OH−

Similarly

∴ [OH−] =

= 4.2426 × 10⁴ M

∴ [H+] = = 2.357 × 10⁻¹¹

Cell reaction

At anode H₂ + 2e−

At cathode + 2e− H₂

———————————————

On applying Nernst equation

Ecell = E°cell −log

Ecell = 0 −log

= 0.0591 log = 0. 4575 V

Example 12

Consider the reaction, 2Ag+ + Cd → 2Ag + Cd ^2+. The standard electrode potentials for Ag+/Ag and Cd²⁺/Cd couples 0.80 V and 0.40 V respectively. (i) What is the standard potential for this reaction? (ii) For the electrochemical cell in which the above reaction takes place which electrode is negative electrode ? (iii) Will the total emf of the given reaction be more negative or positive, if the concentration of Cd²⁺ ions is 0.1 M rather than 1.0 M ?

Solution

(i) In the given reaction Cd is being oxidised to Cd²⁺ ions and Ag+ ions are being reduced to Ag metal. Thus, the galvanic cell in which the given reaction takes place can be represented as

Cd(s) | Cd²⁺(aq) || Ag+(aq) | Ag(s)

Thus, the standard potential of the given reaction would be the standard emf of the above cell (E°cell) which is given by

E°cell = E°Cathode − E°Anode 

= 0.80 − 0.40 = 0.40 V

(ii) Cd(s)|Cd²⁺(aq) electrode constitutes the negative electrode of the cell, since it is the electrode at which oxidation takes place.

(iii) The cell in which the concentration of Cd²⁺ ions is 0.1 M and not 1.0 M can
be shown as

Cd(s) | Cd²⁺(0.1M) || Ag+ (1.0 M) | Ag(s)

Cell reaction Cd(s) + 2Ag+ 2Ag(s) + Cd²⁺(aq)

For this cell, Ecell = E°cell −log

= 0.40 − 0.0295 × log

= 0.40 − 0.0295 × log 10⁻¹

= 0.40 + 0.0295 × 1 = 0.4295 V

Example 13

A zinc rod is placed in 0.1 M solution of ZnSO₄ at 25°C. Assuming that the salt is dissociated to the extent of 95% at this dilution, calculate the potential of the electrode at this temperature. Given that = − 0.76 volts.

Solution

Concentration of ZnSO₄ solution = 0.1 M

Percentage of dissociation of ZnSO₄ solution = 95%

Concentration of Zn2+ ions in ZnSO₄ solution = = 0.095 M

Thus, the electrode can be represented as

Zn(s) | Zn₂+(0.095 M)

Reduction reaction taking place at this electrode is

Zn²⁺ + 2e− → Zn(s) (Here n =2)

According to the Nernst equation, the reduction potential of the above electrode is given by −log

or −0.76 + log 0.095

or −0.79 volt

Example 14

The emf of the cell

Zn | ZnCl₂(0.05 mol dm⁻³) | Cl^– | AgCl(s) | Ag

is 1.015 V at 298 K, the silver electrode being positive, while the temperature coefficient of its emf is −0.000492 VK⁻¹. Write down the equation for the reaction occuring when the cell is allowed to discharge and calculate the changes in (a) free energy (G), and (b) heat content (H) and (c) entropy (S) accompanying this reaction, at 298 K.

Solution

Cell reaction

At anode:

Zn → Zn²⁺ + 2e⁻

At cathode: 2AgCl(s) + 2e− → 2Ag⁺ + 2Cl−

—————————————

Zn + 2AgCl(s) → 2Ag + Zn²⁺ + 2Cl−

(a) The free energy change accompanying the reaction is given by

ΔG = −nFE

n =2, E = 1.015 V, F = 96500 C mol⁻¹

ΔG298 = −2 × 1.015 V × 96500 C mol⁻¹

ΔG298 = −195895 J mol⁻¹

= −195.895 kJ mol¹

(b) ΔH = − nFE + nFT

∴ ΔH298 = −195.895 kJ mol⁻¹ + ΔH298 = −224.20 kJ mol^–1

(c) ΔG = ΔH − T ΔS

ΔS =

ΔS298 = nF

= (−2 × 96500 × 0.000492) JK₁ mol₁

= −95.0 J K−1 mol⁻¹

Example 15

For the following galvanic cell, calculate the emf at 25°C. Assign the correct polarity for the spontaneous reaction to take place

Ag | AgCl(s), KCl (0.2 M) || KBr (0.001 M), AgBr(s) | Ag

The solubility product of AgCl and AgBr are 2.8 × 10⁻¹⁰ and 3.3 × 10⁻¹³ respectively.

Solution

On the basis of the cell as given we have anode as:

Anode: Ag(s) Ag+(c1) + e− (Oxidation)

At cathode : Ag+(c²) + e− Ag(s) (Reduction)

For concentration cell

Ag | AgCl(s), KCl (0.2 M) || KBr (0.001M), AgBr(s) | Ag

Net reaction is

Ag+ (c₂) Ag+(c₁)

For this reaction in above concentration cell

ECell = log₁₀ ….(i)

AgCl Ag+ + Cl−

∴ Ksp of AgCl = [Ag+] [Cl−]

Ksp of AgCl = 2.8 × 10⁻¹⁰ [Cl−] of KCl = 0.2 M

(Because KCl is assumed as 100% ionised)

∴ 2.8 × 10⁻¹⁰ = [Ag+] × 0.2

∴ [Ag+] == 14 × 10−10 M

[Ag+] of AgCl = C1

∴ C1 = 14 × 10¹⁰ M

Now AgBr Ag+ + Br

Ksp of AgBr = [Ag+] [Br−]

Ksp of AgBr = 3.3 × 10⁻¹³

(Because KBr is also assumed as 100 % ionised)

∴ 3.3 × 10−13 = [Ag+] [0.001]

∴ [Ag+] = = 3.3 × 10⁻¹⁰ M

This [Ag+] of AgBr = C₂

∴ C₂ = 3.3 × 10⁻¹⁰ M

Substituting the values of C₁, C₂ and n (n =1) in equation (i), we have

Ecell = 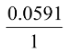log = −0.337 V

Since Ecell has negative value, the cell will not function as it is given. Thus, the polarities will be reversed for the spontaneous reaction. The cell will be constructed as follows.

Ag | AgBr(s) || AgCl(s) | Ag

Example 16

The standard reduction potential of Cu²⁺/Cu and Ag+/Ag electrodes are 0.337 and 0.799 volt respectively. Construct a galvanic cell using these electrodes so that its standard emf is positive. For what concentration of Ag+ will the emf of the cell at 25°C be zero, if the concentration of Cu²⁺ is 0.10 M ?

Solution

Since = 0.799 V is greater than = 0.337 V. Ag+(aq)/Ag(s) will form the cathode and Cu(s)/Cu⁺² (aq) will behave as anode of the galvanic cell. Thus, the cell can be represented as given below. Here M1 is the concentration of Ag+(aq) ions

Cu(s) | Cu2+( 0.01M) || Ag+(c) | Ag(s)

Cell reaction is Cu(s) + 2Ag+(aq) Cu²⁺(aq) + 2Ag(s)

Here n =2

From Nernst equation at 298 K, we have

Ecell = E°cell − log

= [ − ] −0.0295 log

At equilibrium Ecell =0

0.0 = (0.799 − 0.337) − 0.0295 log

0.462 = 0.0295 log

or log = = 15.6610

or = antilog 15.6610 = 4.571 × 10¹⁵

∴ c₂ =

Hence

∴ [Ag+] = 1.47 × 10⁹ M.